Applications of the generalized norm solver

Basic formulation for the linear fitting problem

To verify the $L_1$-norm solver and establish its utility across several geophysical optimization problems, we tested on a series of one-dimensional fitting problems. We began with the simplest fitting problem, a line-fit estimation that would be suitably solved by least-squares line fitting in most cases.

To show the advantages of an $L_1$-based methodology, we injected both Gaussian and non-Gaussian noise. In general, while $L_2$ fitters are well suited to wide-spectrum noise, they are particularly prone to misleading or unphysical results if the noise has many spike- or burst-like. We experimented with a linear fit of a set of data plus several spikes.

The problem setup of the line-fit is similar, but simpler, than the other examples. It serves as a good explanatory case-study of the set-up of a solver. We begin with a data space, ${\bf d}$, representing the noisy sampling of a straight line. We intend to model this line with a very simple, two-element line model - namely, slope and intercept according to the conventional $y = \alpha x + \beta$ formula.

We construct a forward operator, ${\bf L}$, which implements the mapping of this model space onto our recorded data. I n the presence of interfering noise, there will be a deviation between predicted data (${\bf L m}$) and recorded data (${\bf d}$). We have tested our solver to minimize this deviation according to $L_2$, Huber, and hybrid $L_1/L_2$ definitions. This simplified example shows the important ability of the $L_1$-style norms to reject large data outliers.

In this case, we formally define the model space,

$${\bf m} = \begin{bmatrix}\alpha \ \beta \end{bmatrix},$$ (1)

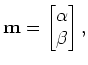where $\alpha$ represents thes slope and $\beta$ represents the y-intercept of a line. And the line operator,

$${\bf L} = \begin{bmatrix}x & 1\end{bmatrix},$$ (2)

We attempt to minimize the objective functions for each defined norm:

$$r_{L_2} = \vert\vert{\bf L m - d}\vert\vert _{L_2},$$

$$r_{L_1} = \vert\vert{\bf L m - d}\vert\vert _{L_1},$$

$$r_{Huber} = \vert\vert{\bf L m - d}\vert\vert _{Huber},$$

$$r_{Hybrid} = \vert\vert{\bf L m - d}\vert\vert _{Hybrid},$$

Because each norm represents a different method for computing the residual, the corresponding minimization has different behaviors with regard to the optimal modeled data. As we will show in the following sections, this impacts the ability of each optimization criterion to produce geophysically useful results in the presence of different types of interference, and for the different characteriestics of the desired function (e.g. sparseness or block-like intervals).

Applications of the generalized norm solver