|
|
|
|
Blocky models via the L1/L2 hybrid norm |
So here we are, embedded in a giant multivariate regression where
we have a bivariate regression (two unknowns).
From the multivarate regression
we are given three vectors in data space.
![]() ,
, ![]() and
and ![]() .
You will recognize these as the current residual, the gradient (
.
You will recognize these as the current residual, the gradient (
![]() ), and the previous step.
(The gradient and previous step appearing here
have previously been transformed to data space
(the conjugate space)
by the operator
), and the previous step.
(The gradient and previous step appearing here
have previously been transformed to data space
(the conjugate space)
by the operator ![]() .)
Our next residual will be a perturbation of the old one.
.)
Our next residual will be a perturbation of the old one.
| (20) |
| (21) |
Let the coefficients
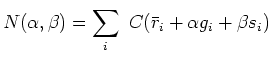 refer to a Taylor expansion of
refer to a Taylor expansion of ![]() about
about ![]() .
.
| (22) |
We have two unknowns,
![]() in a quadratic form.
We set to zero the
in a quadratic form.
We set to zero the ![]() derivative of the quadratic form,
likewise the
derivative of the quadratic form,
likewise the ![]() derivative getting
derivative getting
![$\displaystyle \left[ \begin{array}{c} 0 \ 0 \end{array} \right] \quad=\quad \s...
...array} \right] (\alpha g_i + \beta s_i) \right\} (\alpha g_i + \beta s_i)$](img61.png) |
(23) |
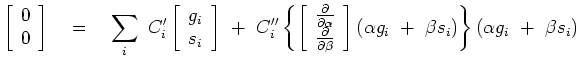 set of equations to solve for
set of equations to solve for
The solution of any 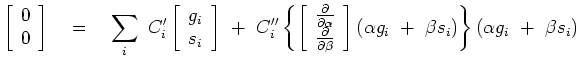 set of simultaneous equations is generally trivial.
The only difficulties arise when the determinant vanishes
which here is easy (luckily) to understand.
Generally the gradient should not point in the direction of the previous step
if the previous move went the proper distance.
Hence the determinant should not vanish.
Practice shows that the determinant will vanish when all the inputs are zero,
and it may vanish if you do so many iterations that you should have stopped already,
in other words when the gradient and previous step are both tending to zero.
set of simultaneous equations is generally trivial.
The only difficulties arise when the determinant vanishes
which here is easy (luckily) to understand.
Generally the gradient should not point in the direction of the previous step
if the previous move went the proper distance.
Hence the determinant should not vanish.
Practice shows that the determinant will vanish when all the inputs are zero,
and it may vanish if you do so many iterations that you should have stopped already,
in other words when the gradient and previous step are both tending to zero.
Using the newly found
![]() , update the residual
, update the residual ![]() at each location
(and update the model).
Then go back to re-evaluate
at each location
(and update the model).
Then go back to re-evaluate
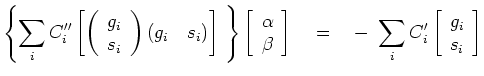 and
and ![]() at the new
at the new ![]() locations.
Iterate.
locations.
Iterate.
In what way do we hope/expect
this new bivariate solver
embedded in a conjugate direction solver
to perform better than old IRLS solvers?
After paying the inevitable price,
a substantial price, of computing
![]() and
and
![]() the iteration above does some serious thinking,
not a simple linearization,
before paying the price again.
the iteration above does some serious thinking,
not a simple linearization,
before paying the price again.
If the convex function ![]() were least squares, subsequent iterations would do nothing.
Although the Taylor series of the second iteration
would expand about different residuals
were least squares, subsequent iterations would do nothing.
Although the Taylor series of the second iteration
would expand about different residuals ![]() than the first iteration,
the new second order Taylor series are the exact representation of the least squares penalty function,
i.e. the same as the first - so the next iteration goes nowhere.
than the first iteration,
the new second order Taylor series are the exact representation of the least squares penalty function,
i.e. the same as the first - so the next iteration goes nowhere.
Will this computational method work (converge fast enough) in the ![]() limit?
I don't know.
Perhaps we'll do better to approach that limit
(if we actually want that limit)
via gradually decreasing the threshold
limit?
I don't know.
Perhaps we'll do better to approach that limit
(if we actually want that limit)
via gradually decreasing the threshold ![]() .
.
|
|
|
|
Blocky models via the L1/L2 hybrid norm |