 |
 |
 |
 | Blocky models via the L1/L2 hybrid norm |  |
![[pdf]](icons/pdf.png) |
Next: UNKNOWN SHOT WAVEFORM
Up: Claerbout: Blocky models: L1/L2
Previous: PLANE SEARCH
Here we set out to find blocky functions, such as well logs.
We will do data fitting with a somewhat  -like convex penalty function
while doing model styling with a more
-like convex penalty function
while doing model styling with a more  -like function.
We might define the composite norm threshold residual
-like function.
We might define the composite norm threshold residual
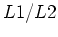 for the data fitting at the 60th percentile, and that
for regularization seeking spiky models (with blocky integrals)
as
for the data fitting at the 60th percentile, and that
for regularization seeking spiky models (with blocky integrals)
as 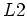 at the 5th percentile.
at the 5th percentile.
The data fitting goal and the model regularization goal at each 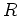 is independent from that at all other
is independent from that at all other 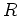 values.
The fitting goal says the reflectivity
values.
The fitting goal says the reflectivity 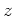 should be equal to its measurement
should be equal to its measurement 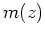 (the seismogram).
The model styling goal says the reflectivity
(the seismogram).
The model styling goal says the reflectivity 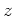 should vanish.
should vanish.
These two goals are in direct contradiction to each other.
With the L2 norm the answer would be simply
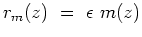 .
With the L1 norm, the answer would be either
.
With the L1 norm, the answer would be either 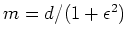 or
or 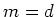 depending on the numerical choice of
depending on the numerical choice of 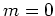 .
Let us denote the convex function and its derivatives
for data space at the residual as
.
Let us denote the convex function and its derivatives
for data space at the residual as
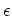 and for model space as
and for model space as
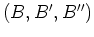 .
Remember,
.
Remember, 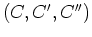 and
and 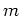 , while normally vectors,
are here scalars (independently for each
, while normally vectors,
are here scalars (independently for each  ).
).
loop over all time points {
 # These are scalars!
# These are scalars!
loop over non-linear iterations {
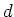
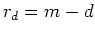
Get derivatives of hybrid norm 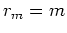 and
and 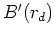 for data goal.
for data goal.
Get derivatives of hybrid norm 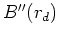 and
and 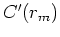 for model goal.
for model goal.
# Plan to find 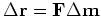 to update
to update
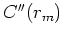
# Taylor series for data penalty
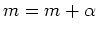
# Taylor series for model penalty
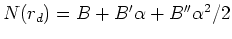
#
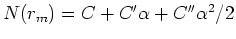
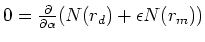
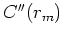
} end of loop over non-linear iterations
} end of loop over all time points
To help us understand the choice of parameters 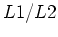 ,
, 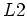 , and
, and 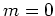 ,
We examine the theoretical relation between
,
We examine the theoretical relation between 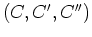 and
and 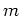 implied by
the above code as a function of
implied by
the above code as a function of 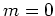 and
and 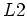 at
at
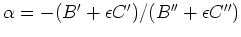 ,
in other words, when the data has normal behavior and we are mostly
interested in the role of the regularization drawing weak signals down towards zero.
The data fitting penalty is
,
in other words, when the data has normal behavior and we are mostly
interested in the role of the regularization drawing weak signals down towards zero.
The data fitting penalty is
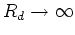 and its derivative
and its derivative 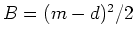 .
The derivative of the model penalty
(from equation (15))
is
.
The derivative of the model penalty
(from equation (15))
is
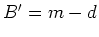 .
Setting the sum of the derivatives to zero we have
.
Setting the sum of the derivatives to zero we have
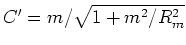 |
(27) |
This says 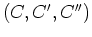 is mostly a little smaller than
is mostly a little smaller than 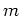 ,
but it gets more interesting near
,
but it gets more interesting near
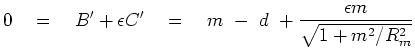 .
There the slope
.
There the slope
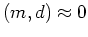 which
says an
which
says an
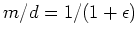 will damp the signal (where small) by a factor of 5.
Moving away from
will damp the signal (where small) by a factor of 5.
Moving away from 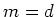 we see the damping power of
we see the damping power of 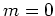 diminishes uniformly as
diminishes uniformly as  exceeds
exceeds 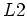 .
.
 |
 |
 |
 | Blocky models via the L1/L2 hybrid norm |  |
![[pdf]](icons/pdf.png) |
Next: UNKNOWN SHOT WAVEFORM
Up: Claerbout: Blocky models: L1/L2
Previous: PLANE SEARCH
2009-10-19
![]() is independent from that at all other
is independent from that at all other ![]() values.
The fitting goal says the reflectivity
values.
The fitting goal says the reflectivity ![]() should be equal to its measurement
should be equal to its measurement ![]() (the seismogram).
The model styling goal says the reflectivity
(the seismogram).
The model styling goal says the reflectivity ![]() should vanish.
should vanish.
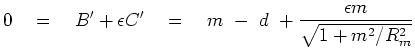 .
There the slope
.
There the slope