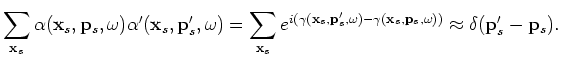|
 |
 |
 | Modeling, migration, and inversion in the generalized source and receiver domain |  |
![[pdf]](icons/pdf.png) |
Next: APPENDIX B
Up: Modeling, migration, and inversion
Previous: Bibliography
This appendix derives the objective function in the encoded source domain. We start with the objective function in the source and receiver domain as follows:
 |
|
|
(A-1) |
From Equation 8, we can also get the inverse phase-encoding transform. For source plane-wave phase encoding,
since the forward operator is unitary, the inverse transform
can be written as follows:
 |
|
|
(A-2) |
For random phase encoding, a similar result can also be obtained, because different realizations of random sequences should be approximately orthogonal,
provided that those random sequences are "sufficiently" random; thus we have
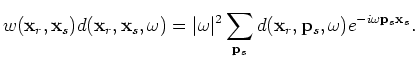 |
|
|
(A-3) |
Therefore, we can use a more general form to express the inverse phase-encoding transform:
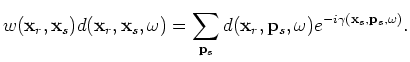 |
|
|
(A-4) |
where for plane-wave phase encoding, 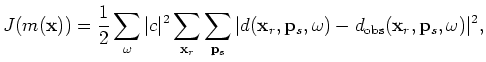 and
and
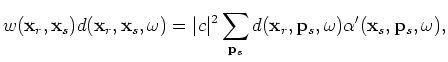 ;
for random phase encoding,
;
for random phase encoding, 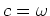 and
and
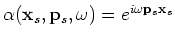 .
.
Substituting Equation A-4 into A-1 yields:
where
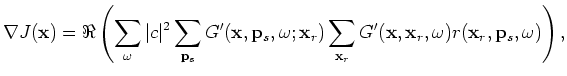 is defined to be the residual in the encoded source domain:
is defined to be the residual in the encoded source domain:
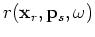 |
|
|
(A-6) |
For plane-wave phase encoding, if the 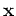 is sampled densely enough,
is sampled densely enough,
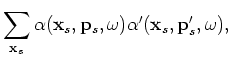 |
|
|
(A-7) |
For random phase encoding, the following property also holds as long as the random sequences are "sufficiently" random:
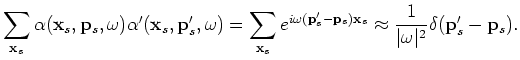 |
|
|
(A-8) |
Substituting Equation A-7 or A-8 into A-5, we get the data-misfit function in the encoded source domain:
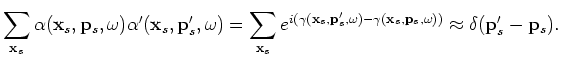 |
|
|
(A-9) |
 |
 |
 |
 | Modeling, migration, and inversion in the generalized source and receiver domain |  |
![[pdf]](icons/pdf.png) |
Next: APPENDIX B
Up: Modeling, migration, and inversion
Previous: Bibliography
2009-04-13
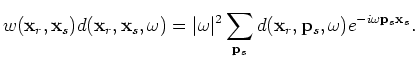
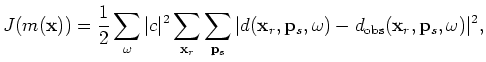 and
and
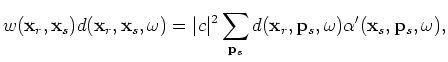 ;
for random phase encoding,
;
for random phase encoding, 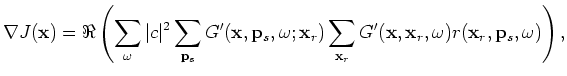 is defined to be the residual in the encoded source domain:
is defined to be the residual in the encoded source domain:
![]() is sampled densely enough,
is sampled densely enough,