|
|
|
|
Joint wave-equation inversion of time-lapse seismic data |
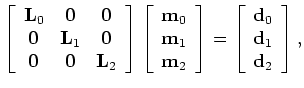 are respectively datasets for the baseline, first and second monitor,
are respectively datasets for the baseline, first and second monitor,
 is the baseline reflectivity and the time-lapse reflectivities
is the baseline reflectivity and the time-lapse reflectivities
 and
and
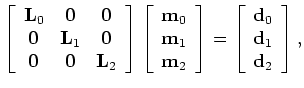 were acquired (with survey geometries defined by the linear
were acquired (with survey geometries defined by the linear
The least-squares solution to equation A-18 is given as
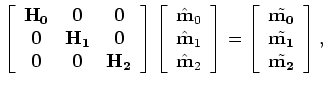 is the migrated image from the
is the migrated image from the
 is the temporal regularization between the surveys.
Note that
is the temporal regularization between the surveys.
Note that
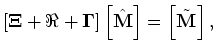 and
and
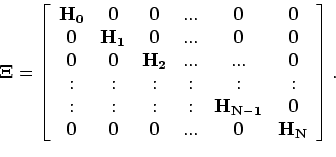 |
(A-26) |
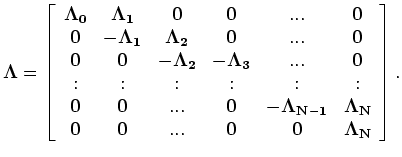 is given as
is given as
 may be set to zero, since it is assumed that the original geological structure is unchanged over time or that geomechanical changes are accounted for before/during inversion.
may be set to zero, since it is assumed that the original geological structure is unchanged over time or that geomechanical changes are accounted for before/during inversion.
|
|
|
|
Joint wave-equation inversion of time-lapse seismic data |