|
|
|
|
Accelerating seismic computations using customized number representations on FPGAs |
Precision and range are key resources to be traded off against the
performance of a computation. We looked at three different types of
number representation: fixed-point, floating-point and logarithmic.
Consider the case when ![]() is represented as a fixed-point
number, with an integer part
is represented as a fixed-point
number, with an integer part ![]() which is
which is ![]() bits in length, and a
fraction part
bits in length, and a
fraction part ![]() which is
which is ![]() bits in length.
bits in length.
|
|
|
The integer bit-width, which represents the dynamic range of the number, is calculated according to equation (1):
| (1) |
For the floating-point number system, let ![]() represent a
floating-point number
represent a
floating-point number
![]() , where
, where ![]() is
the sign bit,
is
the sign bit, ![]() is the mantissa with a bit-width of
is the mantissa with a bit-width of ![]() bits, and
bits, and
![]() is the exponent with a bit-width of
is the exponent with a bit-width of ![]() bits.
bits.
The value of the mantissa ![]() is expressed as:
is expressed as:
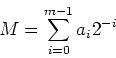 |
(2) |
where
![]() .
.
It is possible to relate the bit-width ![]() of the mantissa of the
node to the error when representing the mantissa by a finite
bit-width
of the mantissa of the
node to the error when representing the mantissa by a finite
bit-width ![]() , as follows:
, as follows:
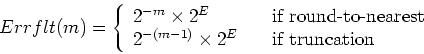
where ![]() is the value of the exponent at the node.
is the value of the exponent at the node.
Since there is no standard to encode logarithmic numbers, in this report we use a fixed-point format to store the logarithmic value.
|
|
|
|
Accelerating seismic computations using customized number representations on FPGAs |