Next: Image Depth in ADCIGs
Up: Reproducible Documents
Traveltime of refracted rays
In this Appendix I derive equations ![[*]](icons/crossref.png) and
and ![[*]](icons/crossref.png) .
From equation
.
From equation ![[*]](icons/crossref.png) we have:
we have:
 |
(1) |
and, from the imaging condition (the sum of the traveltime of the
extrapolated rays at the image point has to be equal to the traveltime
of the multiple) we have
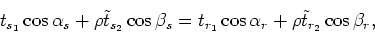 |
(2) |
Solving those two equations for
 and
and
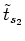 we get
we get
It is interesting to check these equations in two particular cases:
- For a specular multiple from a flat water-bottom, we have
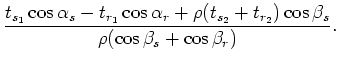 ,
,
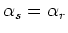 ,
,
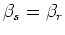 and therefore we get
and therefore we get
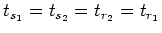 and
and
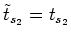 as the geometry of the
problem requires. Notice that this is true for any
as the geometry of the
problem requires. Notice that this is true for any 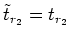 .
.
- For a specular water-bottom multiple migrated with water velocity (
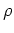 ),
we have
),
we have
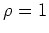 and
and
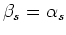 . Furthermore, since
the multiple behaves as a primary,
. Furthermore, since
the multiple behaves as a primary,
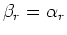 and we again
get
and we again
get
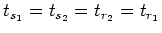 and
and
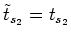 .
.
Next: Image Depth in ADCIGs
Up: Reproducible Documents
2007-10-24
![]() and
and ![]() .
From equation
.
From equation ![]() we have:
we have:
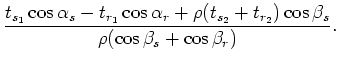 ,
,