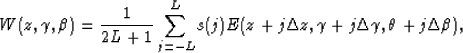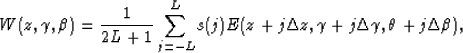Next: 3-D SEG/EAGE salt model
Up: Tang: Imaging in the
Previous: artifacts caused by sparsely
The downward-frowning artifacts observed in the previous section have a great influence on seismic angle-domain processing.
They can destort the final image when we stack over the angle and azimuth axes, generating fake reflectors that can lead to misinterpretation.
They can also affect the accuracy of residual-moveout-based velocity analysis,
since with those frowning curves, it is difficult to predict the residual moveout acurately.
There are four possible methods to get rid of those artifacts in angle gathers:
- 1.
- Define a non-linear transformation in the subsurface-offset
domain to get an artifact-free angle gather.
- 2.
- Densely interpolate the data before migration. This data-space interpolation is very helpful
if the velocity structure is simple, but helps little when the velocity structure is complex.
- 3.
- Apply image-space interpolation. By assuming that reflectivities are changing smoothly along angles and azimuths and that
any abrupt changes in amplitudes are caused by poor illumination or poor sampling,
we can run least-squares inversion with regularization in the angle domain by smoothing along angles and azimuths
to attenuate those artifacts Prucha et al. (2000). Or equivalently, we can run least-squares inversion
with differential-semblence regularization in the subsurface-offset domain Tang (2006); Valenciano (2006).
Both these methods are effective but computationally demanding.
- 4.
- Apply selective stacking by designing filters or weighting functions that ignore those artifacts, stacking
only angles and azimuths with good illumination and dense sampling.
In this paper, I will concentrate mainly on the fourth method and describe a simple
but effective way to design the weighting functions.
As we know, when migrating with the correct migration velocity and with densely sampled and infinite recording geometry,
the events in ADCIGs are aligned horizontally. In 2-D there are horizontal lines in the angle domain;
in 3-D there are flat
planes in the angle and azimuth domain, because with infinite acquisition geometry,
all angles and azimuths should be illuminated.
When we don't have densely sampled and infinite recording geometry,
there are holes in the line in the 2-D case or holes in the plane in the 3-D case.
The shape of holes can be fairly irregular, depending on the recording geometry and the geological structure
of the subsurface. The goal of the method is to attenuate the artifacts and enhance the signal-to-noise ratio of the final image
by stacking only those angles and azimuths that are well illuminated. I first compute the envelope of the 3-D angle
gather, then apply 3-D local smoothing based on equation (7) to the computed envelope to get the
weighting function,
| 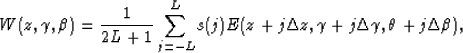 |
(7) |
where W is the weighting function for a particular CMP location.
It is a function of depth z, reflection angle 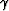 and reflection azimuth
and reflection azimuth 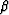 .
E is the envelope function, which can be computed via Hilbert transform.
L is the half length of the moving window, and s(j) determines the shape of the smoothing operator.
In this paper I use a 3-D local boxcar smoothing operator, so s(j)=1.
A more sophisticated smoothing operator, such as a 3-D
local Gaussian smoothing operator, could also be applied.
.
E is the envelope function, which can be computed via Hilbert transform.
L is the half length of the moving window, and s(j) determines the shape of the smoothing operator.
In this paper I use a 3-D local boxcar smoothing operator, so s(j)=1.
A more sophisticated smoothing operator, such as a 3-D
local Gaussian smoothing operator, could also be applied.





Next: 3-D SEG/EAGE salt model
Up: Tang: Imaging in the
Previous: artifacts caused by sparsely
Stanford Exploration Project
5/6/2007