




Next: Oblate Spheroidal Coordinates
Up: Appendix A - 3D
Previous: Appendix A - 3D
The analytic transformation between the elliptic cylindrical and
Cartesian coordinate systems (see example in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
A elliptical coordinate system is specified by,
).
A elliptical coordinate system is specified by,
| ![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_2\\ x_3
\end{array}\rig...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right],\end{displaymath}](img27.gif) |
(8) |
where [x1,x2,x3] are the underlying Cartesian coordinate variables,
![$[\xi_1,\xi_2,\xi_3]$](img28.gif) the RWE elliptic cylindrical coordinates, and
parameter a a stretch parameter controlling the breadth of the
coordinate system.
ECC
the RWE elliptic cylindrical coordinates, and
parameter a a stretch parameter controlling the breadth of the
coordinate system.
ECC
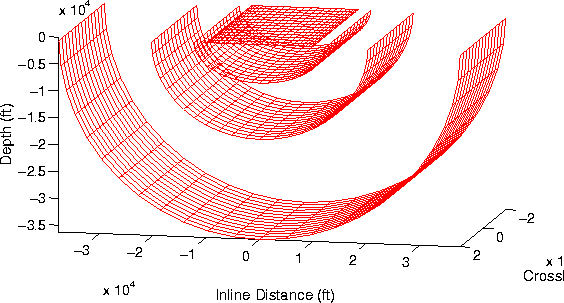
Figure 6 Four sample extrapolation steps of an elliptic
cylindrical coordinate system.

The metric tensor describing the geometry of the elliptic coordinate
system is given by,
| ![\begin{displaymath}
\left[g_{ij}\right] =
\left[\begin{array}
{ccc}
A^2 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & A^2 \\ \end{array}\right],\end{displaymath}](img29.gif) |
(9) |
where 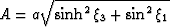 . The
determinant of the metric tensor is:
. The
determinant of the metric tensor is: 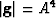 . The associated
(inverse) metric tensor is given by,
. The associated
(inverse) metric tensor is given by,
| ![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{ccc}
A^{-2} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & A^{-2} \\ \end{array}\right],\end{displaymath}](img30.gif) |
(10) |
and weighted metric tensor (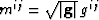 ) is given by,
) is given by,
| ![\begin{displaymath}
\left[m^{ij}\right]
=
\left[\begin{array}
{ccc}
1 & 0 & 0 \\ 0 & A^2 & 0 \\ 0 & 0 & 1 \\ \end{array}\right].\end{displaymath}](img31.gif) |
(11) |
The corresponding extrapolation wavenumber is generated by using
tensors gij and mij in the general wavenumber
expression for 3D non-orthogonal coordinate system
Shragge (2006). Note that even though the elliptic
coordinate system varies spatially, the local curvature parameters
remain constant: n1=n2=n3=0. Thus, inserting the values of
gij, mij and nj leads to the following extrapolation
wavenumber for stepping outward in concentric ellipses 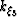 ,
,
|  |
(12) |
The wavenumber for 2D extrapolation in elliptic coordinates reduces to
| 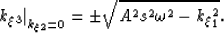 |
(13) |
Note that equation A-5 does not contain a kinematic
approximation of the extrapolation wavenumber.





Next: Oblate Spheroidal Coordinates
Up: Appendix A - 3D
Previous: Appendix A - 3D
Stanford Exploration Project
5/6/2007
![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_2\\ x_3
\end{array}\rig...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right],\end{displaymath}](img27.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
A elliptical coordinate system is specified by,
).
A elliptical coordinate system is specified by,
![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_2\\ x_3
\end{array}\rig...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right],\end{displaymath}](img27.gif)
![\begin{displaymath}
\left[g_{ij}\right] =
\left[\begin{array}
{ccc}
A^2 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & A^2 \\ \end{array}\right],\end{displaymath}](img29.gif)
![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{ccc}
A^{-2} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & A^{-2} \\ \end{array}\right],\end{displaymath}](img30.gif)
![\begin{displaymath}
\left[m^{ij}\right]
=
\left[\begin{array}
{ccc}
1 & 0 & 0 \\ 0 & A^2 & 0 \\ 0 & 0 & 1 \\ \end{array}\right].\end{displaymath}](img31.gif)