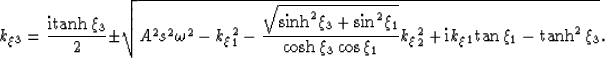Next: About this document ...
Up: Appendix A - 3D
Previous: Elliptic Cylindrical Coordinates
The analytic transformation between the oblate spheroidal and
Cartesian coordinate systems (see example in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A
elliptical coordinate system is specified by,
). A
elliptical coordinate system is specified by,
| ![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_2\\ x_3
\end{array}\rig...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right].\end{displaymath}](img34.gif) |
(14) |
where, again, a is a stretch parameter controlling the breadth of the coordinate system.
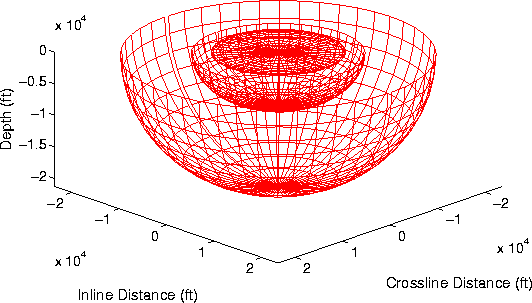
OSC
Figure 7 Three sample extrapolation steps of an oblate
spheroidal coordinate system.

The metric tensor gij describing the geometry of oblate
spheroidal coordinates is given by,
| ![\begin{displaymath}
\left[g_{ij}\right] =
\left[\begin{array}
{ccc}
A^2 & 0 & 0 \\ 0 & B^2 & 0 \\ 0 & 0 & A^2 \\ \end{array}\right],\end{displaymath}](img35.gif) |
(15) |
where 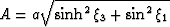 and
and
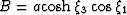 . The determinant of the
metric tensor is:
. The determinant of the
metric tensor is: 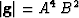 . The associated (inverse) metric
tensor is given by,
. The associated (inverse) metric
tensor is given by,
| ![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{ccc}
A^{-2} & 0 & 0 \\ 0 & B^{-2} & 0 \\ 0 & 0 & A^{-2} \\ \end{array}\right].\end{displaymath}](img38.gif) |
(16) |
and weighted metric tensor is given by,
| ![\begin{displaymath}
\left[m^{ij}\right]
=
\left[\begin{array}
{ccc}
B & 0 & 0 \\ 0 & \frac{A^2}{B} & 0 \\ 0 & 0 & B \\ \end{array}\right].\end{displaymath}](img39.gif) |
(17) |
The corresponding extrapolation wavenumber is generated by inputting
tensors gij and mij into the generalized wavenumber
expression for 3D non-orthogonal coordinate systems
Shragge (2006). Unlike in elliptic cylindrical
coordinates, though, the oblate spheroidal system has
non-stationary ni coefficients: 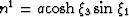 , n2=0 and
, n2=0 and 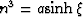 . The resulting
extrapolation wavenumber is
. The resulting
extrapolation wavenumber is
| 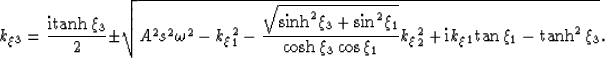 |
(18) |
The wavenumber for 2D extrapolation in elliptic coordinates reduces to
| 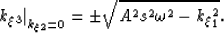 |
(19) |





Next: About this document ...
Up: Appendix A - 3D
Previous: Elliptic Cylindrical Coordinates
Stanford Exploration Project
5/6/2007
![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_2\\ x_3
\end{array}\rig...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right].\end{displaymath}](img34.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A
elliptical coordinate system is specified by,
). A
elliptical coordinate system is specified by,
![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_2\\ x_3
\end{array}\rig...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right].\end{displaymath}](img34.gif)
![\begin{displaymath}
\left[g_{ij}\right] =
\left[\begin{array}
{ccc}
A^2 & 0 & 0 \\ 0 & B^2 & 0 \\ 0 & 0 & A^2 \\ \end{array}\right],\end{displaymath}](img35.gif)
![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{ccc}
A^{-2} & 0 & 0 \\ 0 & B^{-2} & 0 \\ 0 & 0 & A^{-2} \\ \end{array}\right].\end{displaymath}](img38.gif)
![\begin{displaymath}
\left[m^{ij}\right]
=
\left[\begin{array}
{ccc}
B & 0 & 0 \\ 0 & \frac{A^2}{B} & 0 \\ 0 & 0 & B \\ \end{array}\right].\end{displaymath}](img39.gif)