




Next: Discussion
Up: Subsalt reservoir monitoring: Ayeni
Previous: 2D Numerical Example
Claerbout (2004); Tarantola (1987) discuss the use of geophysical inversion as an
imaging tool. In recent applications, inverted seismic images are
computed by weighting
the migration result with the inverse of the Hessian matrix. The
associated large computational cost and complexity makes the explicit
computation of
the Hessian matrix and its inverse impracticable. Valenciano et al. (2006)
demonstrate that by taking the sparsity of the Hessian into account,
the inverse of the Hessian matrix may be computed cheaply and applied
in a target-oriented manner. This approach appears to yield better
results than simple
migration in subsalt reservoirs. For the time-lapse problem, one
approach would be to to compute the time-lapse image as a difference
between
inverse images computed as described above. Another approach would be
to solve for the time-lapse image through inversion rather a
difference between images.
Given a linear modeling operator 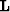 , the synthetic data d
is computed using
, the synthetic data d
is computed using 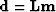 , where m is a
reflectivity model.
Two different surveys (say a baseline and monitor) may be represented as follows:
, where m is a
reflectivity model.
Two different surveys (say a baseline and monitor) may be represented as follows:
| 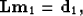 |
(1) |
where 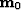 and
and 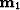 are the reflectivity models at the time we acquire the datasets, (
are the reflectivity models at the time we acquire the datasets, (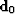 and
and 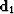 ) respectively.
Taking
) respectively.
Taking 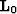 and
and 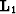 to be the modeling operators
for two different surveys, the quadratic cost functions are defined as
to be the modeling operators
for two different surveys, the quadratic cost functions are defined as
| 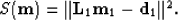 |
(2) |
The least-squares solutions to the problems are given as
| 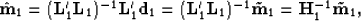 |
(3) |
where 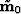 and
and 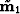 are the migrated
images,
are the migrated
images, 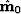 and
and 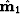 are the
least-squares inverse images,
are the
least-squares inverse images,
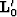 and
and 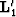 are the migration operators, while
are the migration operators, while
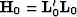 and
and 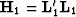 are the Hessian matrices.
are the Hessian matrices.
In the first approach, the inverse time-lapse image (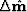 ) is given by
) is given by
| 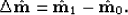 |
(4) |
In the second approach, we express the modeling of operation for the two surveys as follows:
| 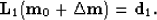 |
(5) |
where 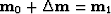 . In matrix form, we can write
. In matrix form, we can write
| ![\begin{displaymath}
\left [ \begin{array}
{cc} {\bf L}_{0} & 0 \\ {\bf L}_{1} &...
...n{array}
{cc} {\bf d}_{0} \\ {\bf d}_{1} \end{array} \right ].\end{displaymath}](img28.gif) |
(6) |
least-squares solution to equation 10 is given as
| ![\begin{displaymath}
\left [ \begin{array}
{cc} {\bf L}'_{0} {\bf L}_{0}+{\bf L}'...
...\tilde {\bf m}_{1} \\ \tilde {\bf m}_{1} \end{array} \right ],\end{displaymath}](img29.gif) |
(7) |
| ![\begin{displaymath}
\left [ \begin{array}
{cc} {\bf H}_{0}+{\bf H}_{1} & {\bf H}...
...\tilde {\bf m}_{1} \\ \tilde {\bf m}_{1} \end{array} \right ].\end{displaymath}](img30.gif) |
(8) |
This, may be re-arranged as follows:
| ![\begin{displaymath}
\left [ \begin{array}
{cc} \hat{{\bf m}}_{0} \\ \Delta \hat...
...\tilde {\bf m}_{1} \\ \tilde {\bf m}_{1} \end{array} \right ].\end{displaymath}](img31.gif) |
(9) |





Next: Discussion
Up: Subsalt reservoir monitoring: Ayeni
Previous: 2D Numerical Example
Stanford Exploration Project
5/6/2007
![]() , the synthetic data d
is computed using
, the synthetic data d
is computed using ![]() , where m is a
reflectivity model.
Two different surveys (say a baseline and monitor) may be represented as follows:
, where m is a
reflectivity model.
Two different surveys (say a baseline and monitor) may be represented as follows:
![]() ) is given by
) is given by
![\begin{displaymath}
\left [ \begin{array}
{cc} \hat{{\bf m}}_{0} \\ \Delta \hat...
...\tilde {\bf m}_{1} \\ \tilde {\bf m}_{1} \end{array} \right ].\end{displaymath}](img31.gif)