Flattening Review

The basic idea behind flattening Lomask (2006) is that the gradient measured at a time (or depth) horizon $\boldsymbol \tau$is equal to the dip $\bf p$ measured at each point of the horizon.

$$\boldsymbol{\nabla} {\boldsymbol \tau}(x,y,t)\quad = \quad {\bf p}(x,y,{\boldsymbol \tau}).$$ (1)

In order to obtain smoothness between horizons a regularization term is added to the problem. Defining the 3-D gradient operator as $\boldsymbol\nabla=[ \frac{\partial }{\partial x} \; \; \frac{\partial }{\partial y} \; \; \frac{\partial }{\partial t} ]^T$a new system of equations can be built,

$${\bf W}_\epsilon\boldsymbol{\nabla}= \left[ \begin{array} {c... ...} \\ \frac{ \partial }{ \partial t} \end{array} \right] \quad ,$$ (2)

where $\bf I$ is the identity matrix and $\epsilon$ is a scaling parameter. The residual is defined as  

$$\bf r \quad = \quad { {\bf W}_\epsilon\boldsymbol{\nabla} \b... ...c}{{\bf p}_x} \\ {{\bf p}_y} \\ {\bf 0} \end{array}\right] }.$$ (3)

The dips need to be measured along the horizon, making the problem non-linear. A Gauss-Newton approach can be used with linearizing about the current estimated horizon volume. Again following the approach of (), we

iterate {  

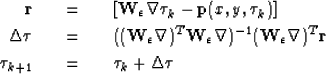$$\begin{eqnarray} \bf r \quad &=& \quad [{\bf W}_\epsilon\boldsymbol{\nabla} \bol... ...bol{\boldsymbol{\tau}}_{k} + \Delta \boldsymbol{\boldsymbol{\tau}}\end{eqnarray}$$ (4) (5) (6)

  }  ,

where the subscript k denotes the iteration number.

Two different approaches can be used for the linearized step (equation 5) The most efficient is to solve the problem a direct inverse in Fourier domain Lomask (2003). When space-domain weighting or model restriction () is needed, a space-domain conjugate gradient approach is warranted.

In general we deal with 2-D angle or offset gathers. The standard approach is to solve a 2-D flattening problem where $\boldsymbol \tau$is a function of time/depth and offset. We revert to a 2-D gradient operator, and solve each CMP/CRP gather independently.