![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . A non-stationary PEF
in the t-x domain is then independently estimated on each shot in Figure
. A non-stationary PEF
in the t-x domain is then independently estimated on each shot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and that PEF is
then used to fill in the missing data in the input and the result is shown in Figure
, and that PEF is
then used to fill in the missing data in the input and the result is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The near offset gap is 4000 feet or 26 traces, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . A non-stationary PEF
in the t-x domain is then independently estimated on each shot in Figure
. A non-stationary PEF
in the t-x domain is then independently estimated on each shot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and that PEF is
then used to fill in the missing data in the input and the result is shown in Figure
, and that PEF is
then used to fill in the missing data in the input and the result is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
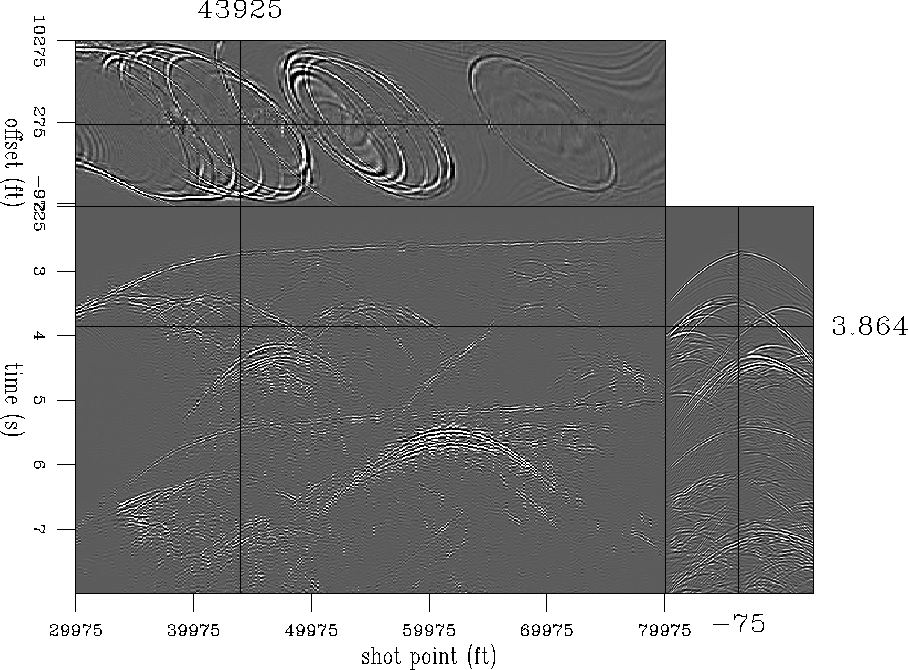 |
The result in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) looks very good. The interpolated portion of the shot on the right side of
Figure
looks very good. The interpolated portion of the shot on the right side of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) looks very good, with diffractions and crossing events correctly interpolated.
Most of the crosstalk present in the pseudo-primaries in Figure
looks very good, with diffractions and crossing events correctly interpolated.
Most of the crosstalk present in the pseudo-primaries in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is gone. However,
there is a sight change in the wavelet, which can be explained by the squaring of the wavelet in the
cross-correlation and the t-x domain PEF capturing spectral information.
is gone. However,
there is a sight change in the wavelet, which can be explained by the squaring of the wavelet in the
cross-correlation and the t-x domain PEF capturing spectral information.
Now looking at the front panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) that corresponds to a constant-offset section,
another problem becomes more apparent. The section looks somewhat jagged from one shot to the next.
This is largely because this problem was solved on a shot-by-shot basis so that there is no guarantee of
lateral continuity between shots. This could be remedied by using a 3D PEF in t,offset, and shot so that
correlations between shots would be taken into account. Another less expensive method would be to use
a non-stationary f-x-y domain PEF Curry (2007), described next.
that corresponds to a constant-offset section,
another problem becomes more apparent. The section looks somewhat jagged from one shot to the next.
This is largely because this problem was solved on a shot-by-shot basis so that there is no guarantee of
lateral continuity between shots. This could be remedied by using a 3D PEF in t,offset, and shot so that
correlations between shots would be taken into account. Another less expensive method would be to use
a non-stationary f-x-y domain PEF Curry (2007), described next.
Instead of interpolating in t-x, we can transform the data into the frequency domain and perform the interpolation individually for each frequency. This approach would largely use the same machinery as the t-x approach, except that all numbers are now complex and the filter would be 2D in shot and offset space. Since this filter does not operate along time or frequency no spectral information is captured, which should eliminate the wavelet issue in the t-x example and the added shot axis (due to the much lower memory requirements of the method) should reduce the jitteriness across the shot axis in the result.
 |
The f-x-y interpolation result, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) does reduce both of these problems. The wavelet now remains consistent
between the recorded data and the interpolated data. The interpolation result also seems less jagged along the shot axis as the PEF is also
estimated along this axis. However, the problem of what appears to be crosstalk is much worse. This is due to assumed stationarity in time.
Since the data were Fourier Transformed as a whole and the problem is solved in the frequency domain, all dips for a given spatial location
appear to be present at all times. This problem could hopefully be addressed by breaking the input data into small time windows that are more
stationary in time.
does reduce both of these problems. The wavelet now remains consistent
between the recorded data and the interpolated data. The interpolation result also seems less jagged along the shot axis as the PEF is also
estimated along this axis. However, the problem of what appears to be crosstalk is much worse. This is due to assumed stationarity in time.
Since the data were Fourier Transformed as a whole and the problem is solved in the frequency domain, all dips for a given spatial location
appear to be present at all times. This problem could hopefully be addressed by breaking the input data into small time windows that are more
stationary in time.