




Next: t-x versus f-x method
Up: Curry: Non-stationary interpolation in
Previous: Introduction
A prediction-error filter (PEF) can be estimated by minimizing the following residual,
| ![\begin{displaymath}
\bold 0
\quad \approx \quad
\bold r =
\left[
\begin{array}
{...
...
{c}
d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \end{array} \right]
,\end{displaymath}](img1.gif) |
(1) |
where fi are unknown filter values and di are known data values. In this
case the filter has two free coefficients and there are seven data points. In
practice, the PEF is multi-dimensional and contains many more coefficients. Once
the PEF has been estimated it can be used in a second least-squares problem
| 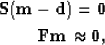 |
|
| (2) |
where 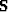 is a selector matrix which is 1 where data
is present and where it is not,
is a selector matrix which is 1 where data
is present and where it is not, 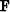 represents convolution with the
PEF and
represents convolution with the
PEF and 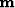 is the desired model. The first line in equation 2
is a hard constraint while the second line is not.
is the desired model. The first line in equation 2
is a hard constraint while the second line is not.
In order for this method to work, the data used as input to equation
1 needs to be similar to the desired output model in equation
2. The slightly different approximations used in t-x and f-x
PEFs are discussed next.





Next: t-x versus f-x method
Up: Curry: Non-stationary interpolation in
Previous: Introduction
Stanford Exploration Project
5/6/2007
![\begin{displaymath}
\bold 0
\quad \approx \quad
\bold r =
\left[
\begin{array}
{...
...
{c}
d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \end{array} \right]
,\end{displaymath}](img1.gif)
![\begin{displaymath}
\bold 0
\quad \approx \quad
\bold r =
\left[
\begin{array}
{...
...
{c}
d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \end{array} \right]
,\end{displaymath}](img1.gif)