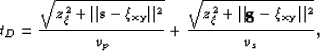
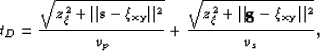 |
(97) |
where ![]() and
and ![]() are the source and receiver vector locations,
respectively. The vector
are the source and receiver vector locations,
respectively. The vector ![]() denotes the point-scatterer location.
The same expression can be represented in midpoint-offset coordinates (
denotes the point-scatterer location.
The same expression can be represented in midpoint-offset coordinates (![]() )
)
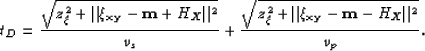 |
(98) |
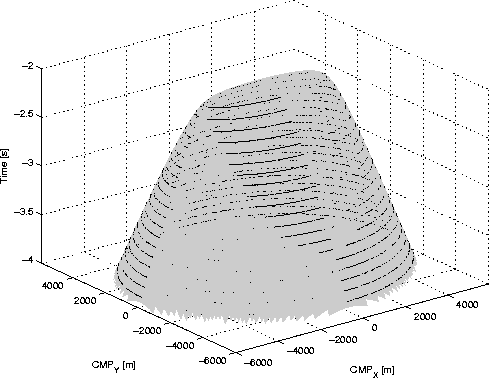
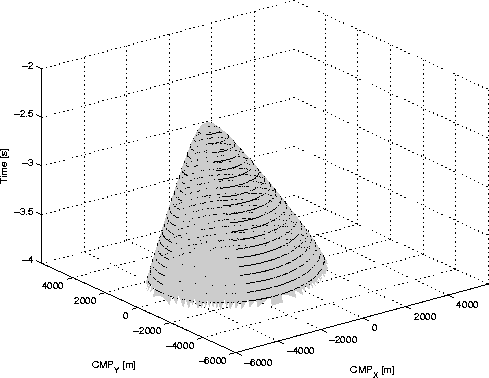
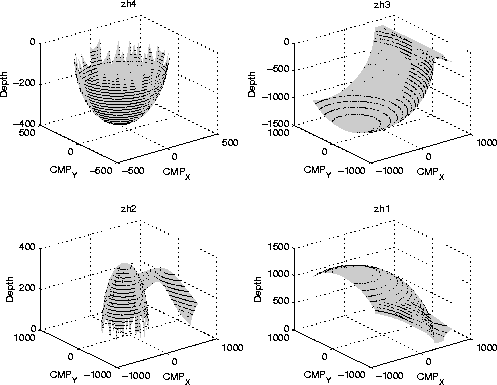
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the single-mode summation
surface in midpoint-offset coordinates for
a point scatterer at a depth of 500 m, a P-velocity
of 3000 m/s, and inline-offset of 3000 m.
Figure
shows the single-mode summation
surface in midpoint-offset coordinates for
a point scatterer at a depth of 500 m, a P-velocity
of 3000 m/s, and inline-offset of 3000 m.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the equivalent surface for converted waves, with an
S-velocity of 1500 m/s.
summation
shows the equivalent surface for converted waves, with an
S-velocity of 1500 m/s.
summation
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for a point scatterer at 500 m of depth in
a medium with constant P-velocity=3000 m/s,
and for an inline-offset=3000 m.
) for a point scatterer at 500 m of depth in
a medium with constant P-velocity=3000 m/s,
and for an inline-offset=3000 m.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for a point scatterer at 500 m of depth in
a medium with constant P-velocity=3000 m/s, and
constant S-velocity=1500m/s, for an
inline-offset=3000 m.
) for a point scatterer at 500 m of depth in
a medium with constant P-velocity=3000 m/s, and
constant S-velocity=1500m/s, for an
inline-offset=3000 m.
The following procedure shows how to go from
![]() to
to ![]() :
:
| |
(99) |
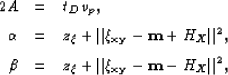 |
||
| (100) |
| (101) |
| (102) |
| (103) |
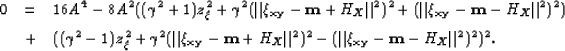 |
||
| (104) |
This can also be writen as follows
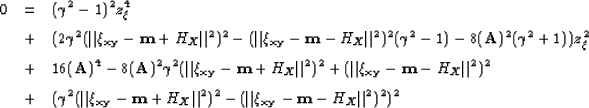 |
||
| (105) |
This polynomial equation has 4 solutions, which take the following well known form:
| (106) |
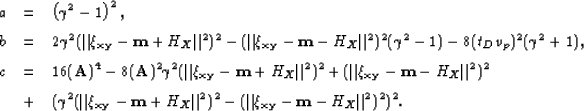 |
||
| (107) |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the four solutions described in the
previous equation. This plot, eventhough is a simple way to verify the
appropiate solution for our case, it's a simple way to select the
solution that is adequate to our problem. The plot suggests that the
fourth solution, that is the solution with the negative both inside
and outside the external square root is the appropiate solution.
presents the four solutions described in the
previous equation. This plot, eventhough is a simple way to verify the
appropiate solution for our case, it's a simple way to select the
solution that is adequate to our problem. The plot suggests that the
fourth solution, that is the solution with the negative both inside
and outside the external square root is the appropiate solution.
 |