![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , from
Chapter 2, extend to 3-D
by replacing the offset and midpoint coordinates for the offset and
midpoint vectors respectively. This extension gives the 3-D expression for the
PS-DMO operator:
, from
Chapter 2, extend to 3-D
by replacing the offset and midpoint coordinates for the offset and
midpoint vectors respectively. This extension gives the 3-D expression for the
PS-DMO operator:
The 2-D PS-DMO operator in equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , from
Chapter 2, extend to 3-D
by replacing the offset and midpoint coordinates for the offset and
midpoint vectors respectively. This extension gives the 3-D expression for the
PS-DMO operator:
, from
Chapter 2, extend to 3-D
by replacing the offset and midpoint coordinates for the offset and
midpoint vectors respectively. This extension gives the 3-D expression for the
PS-DMO operator:
| |
(87) |
where
| |
(88) |
| |
(89) |
and
| |
(90) |
Here, ![]() is the midpoint position vector,
is the midpoint position vector, ![]() is the offset
vector,
is the offset
vector,
![]() is the transformation vector responsible for the CMP to
CRP correction,
and
is the transformation vector responsible for the CMP to
CRP correction,
and ![]() is the vp/vs ratio.
is the vp/vs ratio.
I use the 3-D PS-DMO operator to derive the PS-AMO operator.
Since the vectors ![]() and
and ![]() are collinear, and from substituing
equation
are collinear, and from substituing
equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) into equation
into equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we obtain the first of two time shifts
corresponding to the PS-AMO transformation:
, we obtain the first of two time shifts
corresponding to the PS-AMO transformation:
| |
(91) |
where ![]() corresponds to the intermediate
transformation to zero-offset.
The vector,
corresponds to the intermediate
transformation to zero-offset.
The vector, ![]() , relates to the transformation
from CMP to CRP, which is an
intrinsic property of PS-DMO operator.
, relates to the transformation
from CMP to CRP, which is an
intrinsic property of PS-DMO operator.
The second time shift for the PS-AMO operator corresponds to the transformation from the intermediate zero-offset
position, ![]() , to the final trace position, is
, to the final trace position, is
| |
(92) |
where the vector (![]() ) corresponds to the transformation
from zero-offset to the final CMP position.
The transformation vectors, (
) corresponds to the transformation
from zero-offset to the final CMP position.
The transformation vectors, (![]() and
and ![]() , both comes from equation
, both comes from equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with the offset vector,
with the offset vector, ![]() , equals to the input offset and the output offset, respectively.
, equals to the input offset and the output offset, respectively.
Finally, combining equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I obtain
the expression for the PS-AMO operator:
I obtain
the expression for the PS-AMO operator:
| |
(93) |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that
shows that ![]() and
and ![]() are parallel, as well as
are parallel, as well as
![]() and
and ![]() . Therefore, we can rewrite equation
. Therefore, we can rewrite equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) as
as
| |
(94) |
Both ![]() and
and ![]() can be expressed in terms of the
final midpoint position,
can be expressed in terms of the
final midpoint position,
![]() , by using the rule of sines in the triangle
(
, by using the rule of sines in the triangle
(![]() ,
,![]() ,
,![]() ),
in Figure
),
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , as
, as
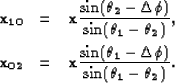 |
(95) | |
| (96) |
By introducing equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) into equation
into equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and by replacing
and by replacing ![]() and
and ![]() for their definition on equation
for their definition on equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
I obtain the final expression for the PS-AMO operator, that is equation
,
I obtain the final expression for the PS-AMO operator, that is equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in
Chapter 4.
in
Chapter 4.