Next: diagonal approximation of Hessian
Up: Tang: Regularized inversion
Previous: bayes inversion
To force the energy in the SODCIGs to concentrate at the zero-offset location, we can pose the problem
as a regularized inversion process, and the objective function is defined as follows:
| 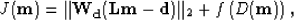 |
(27) |
where 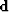 is the recorded data.
is the recorded data.  is a 2-D/3-D wave-equation modeling operator that transforms
the model to prestack data; here I use the adjoint of the Double Square Root (DSR) migration operator.
is a 2-D/3-D wave-equation modeling operator that transforms
the model to prestack data; here I use the adjoint of the Double Square Root (DSR) migration operator.
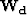 is a mask weight,
which enables us to minimize the data residuals only at known locations, and
is a mask weight,
which enables us to minimize the data residuals only at known locations, and
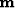 is the model space in terms of
the SODCIGs, a 3-D image cube in the 2-D case and a 5-D image cube in the 3-D case.
Operator
is the model space in terms of
the SODCIGs, a 3-D image cube in the 2-D case and a 5-D image cube in the 3-D case.
Operator 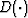 is defined as follows:
is defined as follows:
| 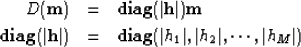 |
(28) |
| (29) |
which is the DSO operator acting along the offset dimension
to penalize energy far from zero-offset locations. Near-offset energy, especially
that around zero-offset locations where 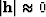 , will not be affected.
After applying DSO, the model-dependent sparseness transform operator
, will not be affected.
After applying DSO, the model-dependent sparseness transform operator 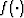 , which minimizes model
residuals in the L1 norm or Cauchy norm, is performed.
The sparseness constraint is applied depth-by-depth and CMP-by-CMP
along the offset dimension. The purpose of adding such a sparseness constraint is to penalize noise which
is typically incoherent and weak, and consequently enhance the resolution of the final inverted result.
, which minimizes model
residuals in the L1 norm or Cauchy norm, is performed.
The sparseness constraint is applied depth-by-depth and CMP-by-CMP
along the offset dimension. The purpose of adding such a sparseness constraint is to penalize noise which
is typically incoherent and weak, and consequently enhance the resolution of the final inverted result.
In fact, adding the DSO regularization term in the SODCIGs is similar to adding a roughener to smooth along
the offset-ray parameters in the ADCIGs. As offset-ray parameters are connected to the offset wavenumbers
via the following equation:
| 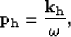 |
(30) |
for a single frequency,
| 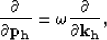 |
(31) |
therefore, for a specific CMP location 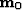 ,
roughening along ray-parameters can be expressed as follows:
,
roughening along ray-parameters can be expressed as follows:
| 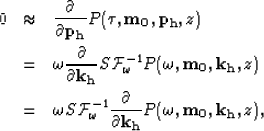 |
(32) |
| (33) |
| (34) |
where S is the slant-stack operator and 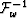 is the
inverse Fourier transform over frequencies. Considering the Fourier duality,
convolving the wavefield
is the
inverse Fourier transform over frequencies. Considering the Fourier duality,
convolving the wavefield 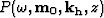 with the differential operator
in the offset-wavenumber domain has the same effect as multiplying the wavefield
with the differential operator
in the offset-wavenumber domain has the same effect as multiplying the wavefield
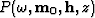 with
with 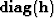 in the offset-space domain:
in the offset-space domain:
| 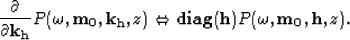 |
(35) |
So smoothing along the offset-ray parameters acts like the DSO regularization term.
Following the discussion in the
previous section, the objective function (27) can be rewritten as follows:
| 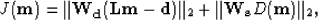 |
(36) |
or more concisely in terms of fitting goals,
| 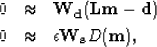 |
(37) |
| (38) |
where 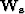 is the diagonal weighting matrix
that forces the sparseness constraints. Here I use the Cauchy norm, thus
is the diagonal weighting matrix
that forces the sparseness constraints. Here I use the Cauchy norm, thus
| 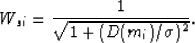 |
(39) |





Next: diagonal approximation of Hessian
Up: Tang: Regularized inversion
Previous: bayes inversion
Stanford Exploration Project
1/16/2007