




Next: regularized least-squares inversion
Up: Tang: Regularized inversion
Previous: introduction
If we let 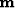 be the model vector and
be the model vector and 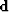 be the data vector, Bayes's theorem would state
be the data vector, Bayes's theorem would state
| 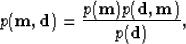 |
(1) |
where 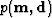 is the distribution of the model parameters posterior to the data
is the distribution of the model parameters posterior to the data 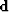 ,expressing the likelihood of the model
,expressing the likelihood of the model 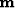 for a given data
for a given data 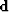 ;
;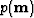 is the probability distribution of the model
is the probability distribution of the model 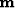 , representing the
prior information about the model; and
, representing the
prior information about the model; and 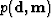 describes how knowledge of the data modifies
the prior knowledge. The quantity
describes how knowledge of the data modifies
the prior knowledge. The quantity 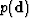 is the probability distribution of the data
is the probability distribution of the data 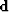 ,
which is a constant for a given data
,
which is a constant for a given data 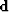 ; thus
; thus 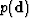 can be seen as a scaling factor Ulrych et al. (2001).
Therefore, equation (1) can be simplified as
can be seen as a scaling factor Ulrych et al. (2001).
Therefore, equation (1) can be simplified as
| 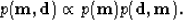 |
(2) |
In the presence of noise, the recorded data 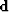 can be expressed as follows:
can be expressed as follows:
| 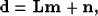 |
(3) |
where 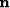 is the noise vector. The likelihood function
is the noise vector. The likelihood function 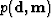 is constructed by
taking the difference between the observed data and the modeled data, thus
is constructed by
taking the difference between the observed data and the modeled data, thus
| 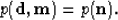 |
(4) |
If we assume the noise has a Gaussian distribution with a zero mean and variance 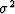 , its
probability function can be written as follows:
, its
probability function can be written as follows:
| 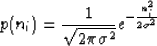 |
(5) |
If each component of the noise vector is independent and
the variance of each noise sample remains constant, the total
probability of the noise vector is
| 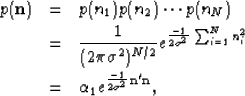 |
(6) |
| (7) |
| (8) |
where 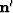 is the adjoint of
is the adjoint of 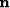 . If we further assume that the model parameters
. If we further assume that the model parameters 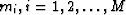 have a Gaussian distribution with a zero mean and a variance
have a Gaussian distribution with a zero mean and a variance 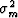 and are independent, the probability
of
and are independent, the probability
of 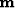 then is
then is
| 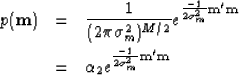 |
(9) |
| (10) |
Plugging equations (8) and (10) into equation (2) yields the following posterior distribution:
| 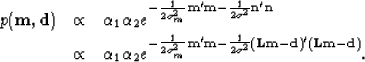 |
(11) |
| (12) |
Since the posterior probability 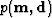 is a quantity describing the probability that the model is correct
given a certain set of observations, we would like it to be maximized. Maximizing the posterior function is
equivalent to finding the minimum of the following objective function:
is a quantity describing the probability that the model is correct
given a certain set of observations, we would like it to be maximized. Maximizing the posterior function is
equivalent to finding the minimum of the following objective function:
| 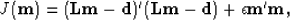 |
(13) |
where 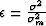 . We can see that if the model parameters are assumed to
have a Gaussian distribution, the solution of maximum posterior probability under Bayes's theorem is equivalent to
the damped least-squares solution. Thus, Bayesian inversion gives another perspective on the same problem,
where minimizing the model residuals in the L2 norm corresponds to a Gaussian prior probability distribution.
As the Gaussian distribution is a short-tailed function that is tightly centered around the mean, it will
result in a smooth solution. Therefore, when a sparse solution is required, the L2
norm is no longer appropriate, and long-tailed distribution functions such as the exponential and Cauchy distributions
should be chosen for the prior probability distribution of
. We can see that if the model parameters are assumed to
have a Gaussian distribution, the solution of maximum posterior probability under Bayes's theorem is equivalent to
the damped least-squares solution. Thus, Bayesian inversion gives another perspective on the same problem,
where minimizing the model residuals in the L2 norm corresponds to a Gaussian prior probability distribution.
As the Gaussian distribution is a short-tailed function that is tightly centered around the mean, it will
result in a smooth solution. Therefore, when a sparse solution is required, the L2
norm is no longer appropriate, and long-tailed distribution functions such as the exponential and Cauchy distributions
should be chosen for the prior probability distribution of 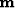 .
.
If we keep equation (8) unchanged and assume 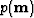 satisfies the exponential probability
distribution, with a mean of zero:
satisfies the exponential probability
distribution, with a mean of zero:
| 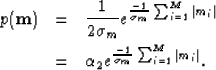 |
(14) |
| (15) |
Then the a posteriori probability becomes
| 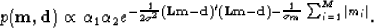 |
(16) |
Finding the maximum of the above function is equivalent to finding the minimum of the following objective function:
| 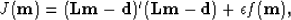 |
(17) |
where 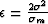 , and the regularization term,
, and the regularization term, 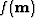 , is defined by
, is defined by
| 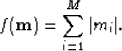 |
(18) |
Therefore, by adding an L1 norm regularization term to the least-squares problem, we get a sparse solution
of the model parameters.
Though minimizing the objective function (17) results in a non-linear problem, it can be solved efficiently
by Iteratively Re-weighted Least-Squares (IRLS). The gradient of the regularization term is
| 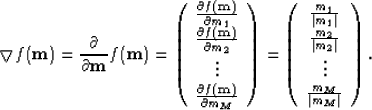 |
(19) |
Therefore the regularization term 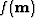 , which minimizes the residual in the L1 norm, can be solved
in the L2 norm by introducing a diagonal weighting function
, which minimizes the residual in the L1 norm, can be solved
in the L2 norm by introducing a diagonal weighting function 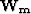 :
:
| 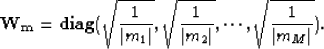 |
(20) |
Then the objective function (17) can be changed to
| 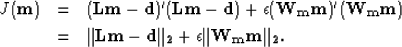 |
(21) |
| (22) |
The derivation of the objective function for the a priori case with a Cauchy distribution is similar, except
the diagonal weighting function changes to the following:
| 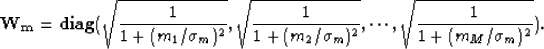 |
(23) |
Since 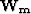 is a function of the model
is a function of the model 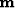 , if we use the gradient-based IRLS method to solve the objective
function (22), we have to recompute the weight
, if we use the gradient-based IRLS method to solve the objective
function (22), we have to recompute the weight 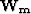 at each iteration and the algorithm can be summarized as
follows:
at each iteration and the algorithm can be summarized as
follows:
- 1.
- At the first iteration,
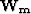 is set to be the identity matrix:
is set to be the identity matrix:
| 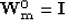 |
(24) |
- 2.
- At the kth iteration, we solve the following fitting goals:
| 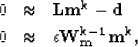 |
(25) |
| (26) |
where Wmik-1 = (|mik-1|)-1/2 in the case of the L1 norm,
or ![$W_{mi}^{k-1} = \left[ 1+\left(\frac{m_i^k}{\sigma_m}\right)^2\right]^{-1/2}$](img35.gif) in the case of the Cauchy norm.
in the case of the Cauchy norm.





Next: regularized least-squares inversion
Up: Tang: Regularized inversion
Previous: introduction
Stanford Exploration Project
1/16/2007
![]() be the model vector and
be the model vector and ![]() be the data vector, Bayes's theorem would state
be the data vector, Bayes's theorem would state
![]() can be expressed as follows:
can be expressed as follows:
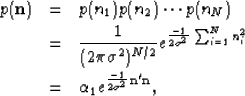
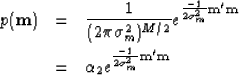
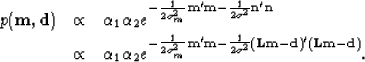
![]() satisfies the exponential probability
distribution, with a mean of zero:
satisfies the exponential probability
distribution, with a mean of zero:
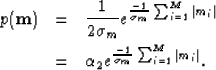
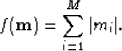
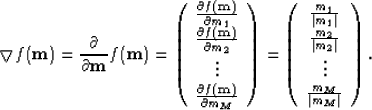
![]() is a function of the model
is a function of the model ![]() , if we use the gradient-based IRLS method to solve the objective
function (22), we have to recompute the weight
, if we use the gradient-based IRLS method to solve the objective
function (22), we have to recompute the weight ![]() at each iteration and the algorithm can be summarized as
follows:
at each iteration and the algorithm can be summarized as
follows: