Anisotropic velocity spectra computation

We compute the anisotropic velocity spectra for the two migration velocity models at a depth equal to the imaged depth (i.e. $z_{\xi}$); the aperture range used is $\left[ -74^{\circ}; 74^{\circ} \right]$, and no weight is applied when summing along the RMO curves. Figures 6 and 7 present secions of the anisotropic velocity spectra cube, whose axes are $\rho_{V_V}$, $\rho_{V_H}$ and $\rho_{V_N}$. In each figure, the three different slices correspond to cube slices at the correct velocity perturbations (for figure 6, $\rho_{V_V}=0.99$, $\rho_{V_H}=0.99$ and $\rho_{V_N}=0.99$; for figure 7, $\rho_{V_V}=0.9$, $\rho_{V_H}=0.9$ and $\rho_{V_N}=0.9$).

 

VelSpec-slice-rho.99-taylor-taylor-flat Figure 6 Velocity Spectra obtained when a constant anisotropic velocity was perturbed by $\rho_V=0.99$.

 

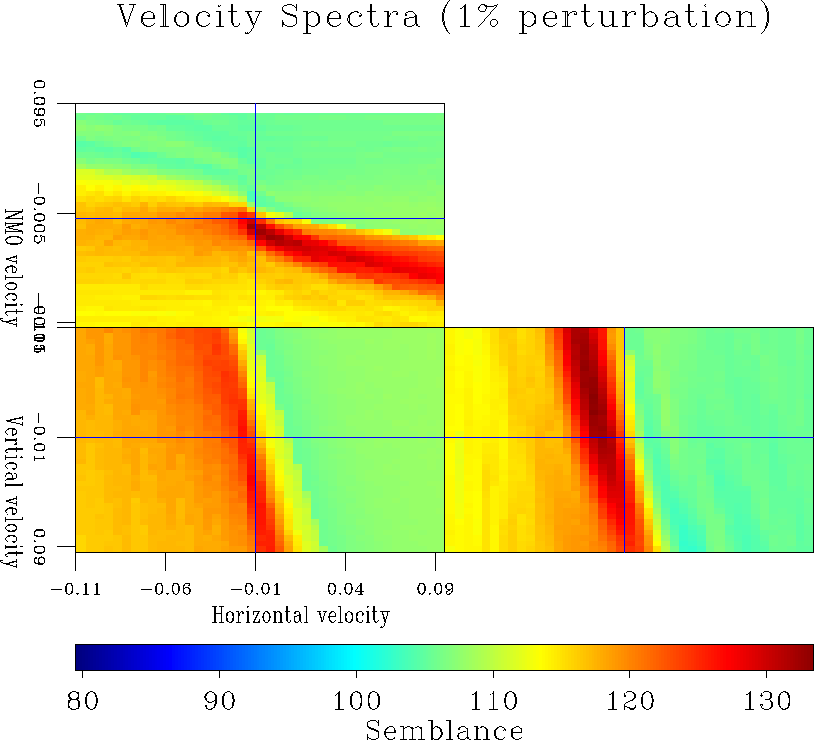VelSpec-slice-rho.9-taylor-taylor-flat Figure 7 Velocity Spectra obtained when a constant anisotropic velocity was perturbed by 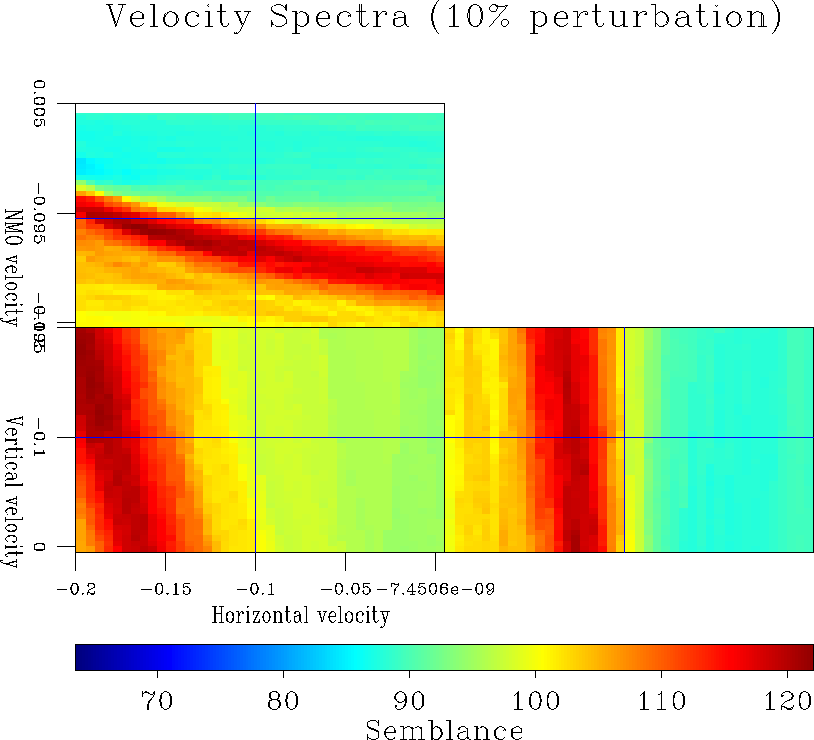$\rho_V=0.9$.

Figures 6 and 7 illustrate that the anisotropic velocity spectra provide accurate estimates of the velocity parameters for small initial velocity perturbations. The accuracy of the estimates then deteriorates as the initial velocity perturbation increases. The bias in the perturbation estimates is due to the fact that the linearized expression of the residual moveout is only a first-order approximation. As illustrated in figures 4 and 5, the linearized formula underestimates the real moveout. Consequently, perturbation estimates from the velocity spectra are of larger magnitude than the true initial perturbations.

Furthermore, the different slices of the velocity spectra show that vertical velocity is by far the most poorly constrained parameter. However, assuming the vertical velocity is determined, the upper panel shows a trade-off between the estimates of $\rho_{V_H}$ and $\rho_{V_N}$ that is approximately linear.

Finally, we estimate the initial anisotropic migration velocity perturbations, =$\left(\rho_V_V,\rho_V_H,\rho_V_N\right)$,by picking the maxima of the semblance cubes, =$\left(\tilde{\rho_{V_V}} ,\tilde{\rho_{V_H}},\tilde{\rho_{V_H}}\right)$. The updated velocity parameters are given by $\frac{_\rho{\bf V}}{\mathbf{\tilde{\rho}}}$,where $_\rho{\bf V}$ is the vector of starting anisotropic migration velocities. It is then possible to remigrate the data with our new estimates of the anisotropic parameters and proceed to a new MVA. Note that after MVA, the the new perturbation, $\mathbf{\hat{\rho}}$ is given by $\frac{\mathbf{\rho}}{\mathbf{\tilde{\rho}}}$.

The following table illustrates the results of the updating process for the two different synthetic cases presented above. It shows that the overall estimation of the anisotropic parameters after picking the maxima of the semblance cubes.

perturbation perturbation perturbation

$$\rho=\left(\rho_V_V,\rho_V_H,\rho_V_N\right) \tilde{\rho}=\left(\tilde{\rho_{V_V}},\tilde{\rho_{V_H}},\tilde{\rho_{V_H}}\right)$$

$$\left(0.99,0.99,0.99\right) \left(1.005,0.985,0.995\right) \left(0.985,1.005,0.995\right)$$ 1% Perturbation

$$\left(0.90,0.90,0.90\right) \left(0.96,0.80,0.93\right) \left(0.9375,1.125,0.968\right)$$ 10% Perturbation