




Next: Appendix B: Crack-influence Decomposition
Up: Appendix A: Bounds and
Previous: Peselnick-Meister-Watt (PMW) Bounds for
The results obtained for self-consistent estimates
can be written in many different ways (Berryman, 2005). We take the self-consistent estimate for bulk modulus to be
| 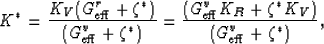 |
(34) |
where
| 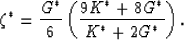 |
(35) |
In (35), K* is determined by (34), depending
also on G*;
G* is determined by the self-consistent expression for the
shear modulus to follow, also depending on K*;
and 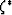 is then determined by (35).
The final result for G* = G*hex in polycrystals having grains with
hexagonal symmetry is
is then determined by (35).
The final result for G* = G*hex in polycrystals having grains with
hexagonal symmetry is
| ![\begin{displaymath}
\frac{1}{G_{\rm hex}^* + \zeta^*} =
\frac{1}{5}\left[\frac{...
...+ \frac{2}{C_{44}+\zeta^*} + \frac{2}{C_{66}+\zeta^*}\right].
\end{displaymath}](img108.gif) |
(36) |
These formulas can be successfully solved by iteration, starting for
example by using values corresponding to upper or lower bounds for the
values of K* and G*.
Some details of the derivation of these formulas can be found in
Willis (1977, 1981) and Berryman (2005).





Next: Appendix B: Crack-influence Decomposition
Up: Appendix A: Bounds and
Previous: Peselnick-Meister-Watt (PMW) Bounds for
Stanford Exploration Project
1/16/2007