




Next: Self-consistent Estimates for Hexagonal
Up: Appendix A: Bounds and
Previous: Voigt and Reuss Bounds
Hashin-Shtrikman-style bounds (Hashin and Shtrikman, 1962a,b; 1963)
on the bulk and shear moduli of isotropic random polycrystals
composed of grains having hexagonal symmetry
have been derived by Peselnick and Meister (1965), with corrections made later by Watt and Peselnick (1980). We will term these the PMW (for Peselnick-Meister-Watt) or the
HS (Hashin-Shtrikman) bounds interchangably. The PMW notation
was similar to that in the original Hashin-Shtrikman paper
on random polycrystals of grains having cubic symmetry
(Hashin and Shtrikman, 1962b). We will use a slightly modified notation here, taking into account
the product formulas (Berryman, 2004b) in order to simplify the statement of the results. Derivations
are found in the references, and therefore not repeated here.
Parameters used to optimize the Hashin-Shtrikman bounds are
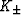 and
and 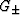 , which have the significance of being the bulk and shear
moduli of two (
, which have the significance of being the bulk and shear
moduli of two (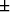 ) isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Simplified formulas for the bulk modulus bounds are:
) isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Simplified formulas for the bulk modulus bounds are:
| 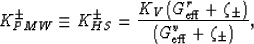 |
(27) |
where
| 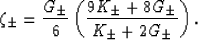 |
(28) |
In (28), the values of 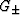 and
and 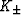 are those
defined algorithmically according to:
are those
defined algorithmically according to:
| 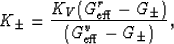 |
(29) |
where, for K-,
| 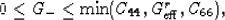 |
(30) |
and, similarly, for the K+ formula,
| 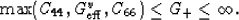 |
(31) |
The corresponding formulas for shear modulus bounds 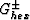 are
are
| ![\begin{displaymath}
\frac{1}{G_{\rm hex}^\pm + \zeta_\pm} =
\frac{1}{5}\left[\f...
...rac{2}{C_{44}+\zeta_\pm} + \frac{2}{C_{66}+\zeta_\pm}\right],
\end{displaymath}](img101.gif) |
(32) |
where the constants 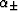 and
and 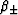 are defined by
are defined by
| 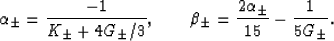 |
(33) |
Peselnick and Meister (1965) had originally obtained all
the results for hexagonal symmetry, except for an additional condition
that permits C44 to be replaced in some
circumstances by 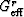 . This condition was added later
by Watt and Peselnick (1980).
. This condition was added later
by Watt and Peselnick (1980).





Next: Self-consistent Estimates for Hexagonal
Up: Appendix A: Bounds and
Previous: Voigt and Reuss Bounds
Stanford Exploration Project
1/16/2007
![]() and
and ![]() , which have the significance of being the bulk and shear
moduli of two (
, which have the significance of being the bulk and shear
moduli of two (![]() ) isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Simplified formulas for the bulk modulus bounds are:
) isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Simplified formulas for the bulk modulus bounds are:
![]() . This condition was added later
by Watt and Peselnick (1980).
. This condition was added later
by Watt and Peselnick (1980).