




Next: Differential N-D Mesh Generation
Up: Shragge: Differential gridding methods
Previous: Introduction
The goal of most grid generation methods is to find the transformation
from a regular computational mesh defined by 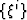 on a
domain
on a
domain 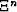 to an irregular grid defined by
to an irregular grid defined by 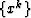 on domain
Xn+l. Usually, the only a priori information is the
location of the mesh boundary points (i.e.
on domain
Xn+l. Usually, the only a priori information is the
location of the mesh boundary points (i.e. 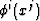 on
on 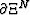 ). Hence, grid generation is a two-fold task: propagate
the boundary values into the interior in a physically consistent
manner, and generate meshes with appropriate attributes
(e.g. well-formed, smooth and non-singular). Thus, two important
questions are by what physical principles are the boundary values
propagated into the interior? And by what manner is the mesh
regularized to ensure that it has acceptable attributes?
). Hence, grid generation is a two-fold task: propagate
the boundary values into the interior in a physically consistent
manner, and generate meshes with appropriate attributes
(e.g. well-formed, smooth and non-singular). Thus, two important
questions are by what physical principles are the boundary values
propagated into the interior? And by what manner is the mesh
regularized to ensure that it has acceptable attributes?
An answer to the first query is found by recasting grid
generation as a Dirchelet BVP: given the boundary values of the mesh,
solve an elliptic Laplace's equation on the mesh's interior.
Mathematically, this requires solving the following system of
equations,
| ![\begin{displaymath}
D^{\xi}[s^j] = 0, \quad \; \quad \Gamma [\xi^i] = \left. \xi...
...right\vert _{\partial S} = \phi^i[s^j], \quad \; \quad i,j=1,n \end{displaymath}](img7.gif) |
(1) |
where ![$D^{\xi}[v]$](img8.gif) is a generalized Laplacian operator acting on field
v in coordinates
is a generalized Laplacian operator acting on field
v in coordinates 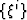 , and
, and 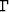 is a projection
operator that maps boundary values
is a projection
operator that maps boundary values ![$\phi^i[s^j]$](img10.gif) of intermediate
domain Sn onto the boundaries of initial domain
of intermediate
domain Sn onto the boundaries of initial domain 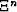 . More
specifically, a BVP is formed for each coordinate component
. More
specifically, a BVP is formed for each coordinate component 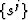 , which requires finding N solutions. Generally, this is an
iterative process that continues until the coordinate fields in
, which requires finding N solutions. Generally, this is an
iterative process that continues until the coordinate fields in 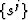 converge to those of
converge to those of 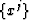 to within some level of
tolerance.
to within some level of
tolerance.
Division of the coordinate fields into independent BVPs, though, does
not permit mesh regularization because coordinate fields are subject
to geometric coupling. Because we wish to generate meshes over
generalized spaces, we must represent this coupling through
differential geometry. Importantly, this provides us with a powerful
set of tools for mesh generation because it: i) specifies a metric
(literally!) for evaluating mesh characteristics (e.g. extent and
orientation of grid clustering); and ii) permits the introduction of
monitor metrics that enable local mesh regularization. These two
topics are discussed in the following two sections.