




Next: Differential 2-D Mesh Generation
Up: Theoretical Overview
Previous: Differential N-D Mesh Generation
Monitor functions are a useful tool for regularizing meshes because
they can establish a metric of minimal quality that prevents
problematic grid clustering. (A simple scalar analog is preventing
division by zero by adding a small number to the denominator.)
Monitor functions can be introduced into
equations 4 and 5 by adding additional
components to the metric tensor,
| 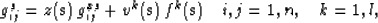 |
(6) |
where gijs is the regularized metric tensor, gxsij is the
unregularized metric tensor calculated by equations 3,
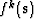 are functions of coordinate
are functions of coordinate 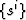 that
provide metric stabilization, and
that
provide metric stabilization, and 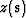 and
and
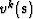 are weighting functions. Hence, where gijxs
tends to zero, functions
are weighting functions. Hence, where gijxs
tends to zero, functions 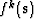 are set to non-zero values.
Note that the functions and their corresponding weights are specified
on a point-by-point basis allowing for localized mesh regularization,
and that the functions should have zero values and derivatives on the
boundary so as to not regularize the boundary geometry.
are set to non-zero values.
Note that the functions and their corresponding weights are specified
on a point-by-point basis allowing for localized mesh regularization,
and that the functions should have zero values and derivatives on the
boundary so as to not regularize the boundary geometry.
Incorporating monitor functions into the Laplacian equation framework
requires altering equations 4. Accordingly, the N-D
differential method gridding equations incorporating monitor functions
are given by,
| ![\begin{eqnarray}
D^{\xi}[s^j] = - D^{\xi} [ f^k ] \frac{\partial f^k}{\partial s...
...rtial S^n}
= \phi^i \left[ \mathbf{s} \right], & \quad i=1,n, & \,\end{eqnarray}](img29.gif) |
(7) |
| (8) |
where 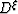 is specified in equation 4 above.
Liseikin (2004) provides theoretical justification of a number of
different approaches to control grid clustering through the
manipulation of monitor functions. In this paper, I use a fairly
basic approach where the monitoring function is specified by a scaled
spatially variant metric determinant.
is specified in equation 4 above.
Liseikin (2004) provides theoretical justification of a number of
different approaches to control grid clustering through the
manipulation of monitor functions. In this paper, I use a fairly
basic approach where the monitoring function is specified by a scaled
spatially variant metric determinant.





Next: Differential 2-D Mesh Generation
Up: Theoretical Overview
Previous: Differential N-D Mesh Generation
Stanford Exploration Project
4/5/2006
![\begin{eqnarray}
D^{\xi}[s^j] = - D^{\xi} [ f^k ] \frac{\partial f^k}{\partial s...
...rtial S^n}
= \phi^i \left[ \mathbf{s} \right], & \quad i=1,n, & \,\end{eqnarray}](img29.gif)