| |
(1) |
| |
(2) | |
| (3) |
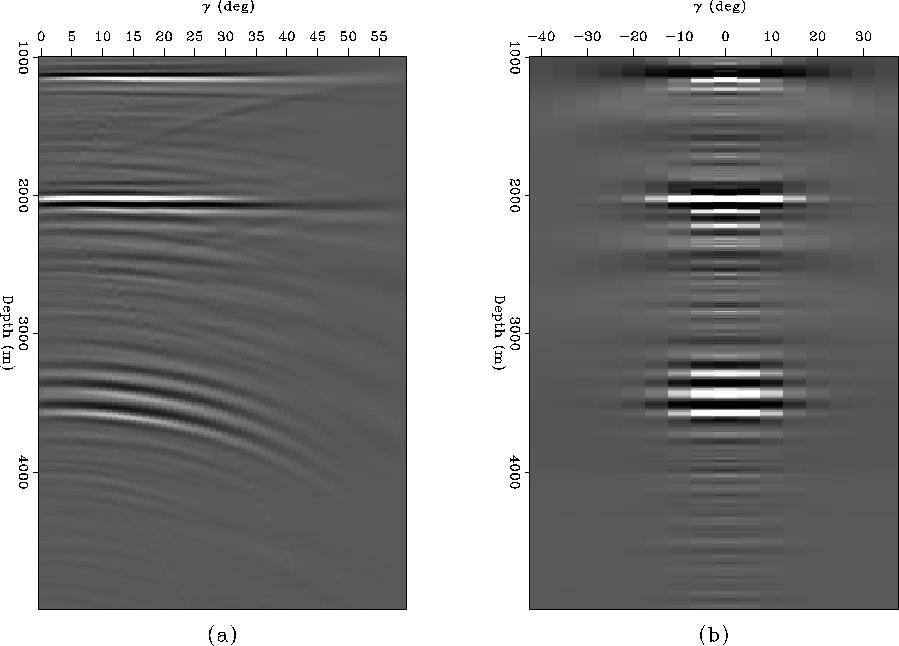
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the inline component of the
pseudo
ADCIG corresponding to the same SODCIG shown in Figure
shows the inline component of the
pseudo
ADCIG corresponding to the same SODCIG shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The primaries are flat and the multiples exhibit a similar residual
moveout as that seen in 2D ADCIGs Biondi and Symes (2004). Panel (b) of
Figure
.
The primaries are flat and the multiples exhibit a similar residual
moveout as that seen in 2D ADCIGs Biondi and Symes (2004). Panel (b) of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the crossline component of the same pseudo 3D ADCIG. Since the
crossline aperture is small, there is very little discrimination between the
primaries and the multiples. This, of course means that using pseudo 3D ADCIGs
to attenuate the multiples relies entirely on the inline direction and is
therefore essentially a 2D process.
shows the crossline component of the same pseudo 3D ADCIG. Since the
crossline aperture is small, there is very little discrimination between the
primaries and the multiples. This, of course means that using pseudo 3D ADCIGs
to attenuate the multiples relies entirely on the inline direction and is
therefore essentially a 2D process.
|
adcigs
Figure 15 Inline component (a) and crossline component (b) of the pseudo 3D ADCIG corresponding to the SODCIG shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . .
|  |