Transformation to true 3D ADCIGs

The mathematical formalism and the methodology for computing true 3D ADCIGs as a function of the aperture angle 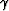$\gamma$ and the data azimuth 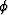$\phi$was given by Biondi and Tisserant 2004. They showed that the ADCIGs as a function of the aperture angle, for a fixed azimuth, may depart from flat even for migration using the correct velocity. As function of azimuth, the curvature of the events increase with increasing aperture angle. For a fixed depth, this translates into an azimuth rotation which depends on the dip of the reflector at that depth.

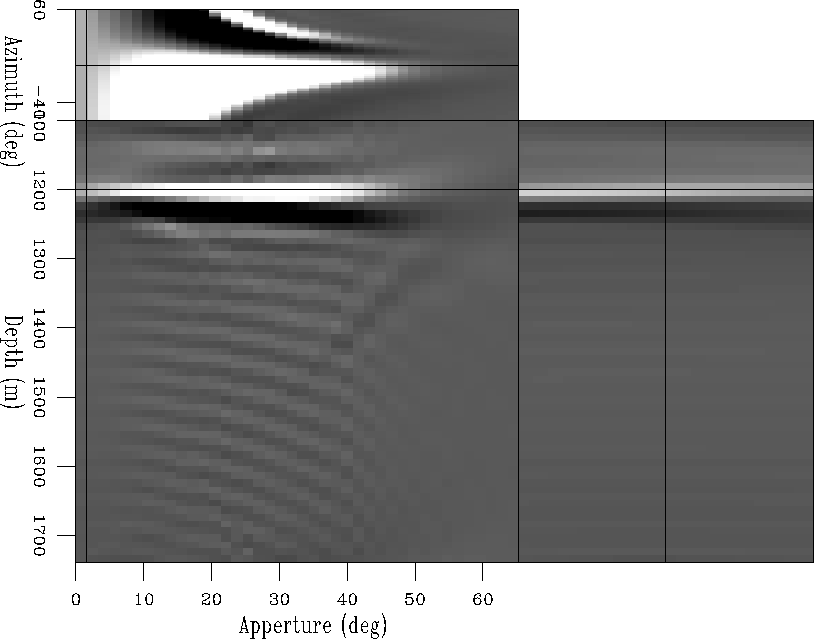
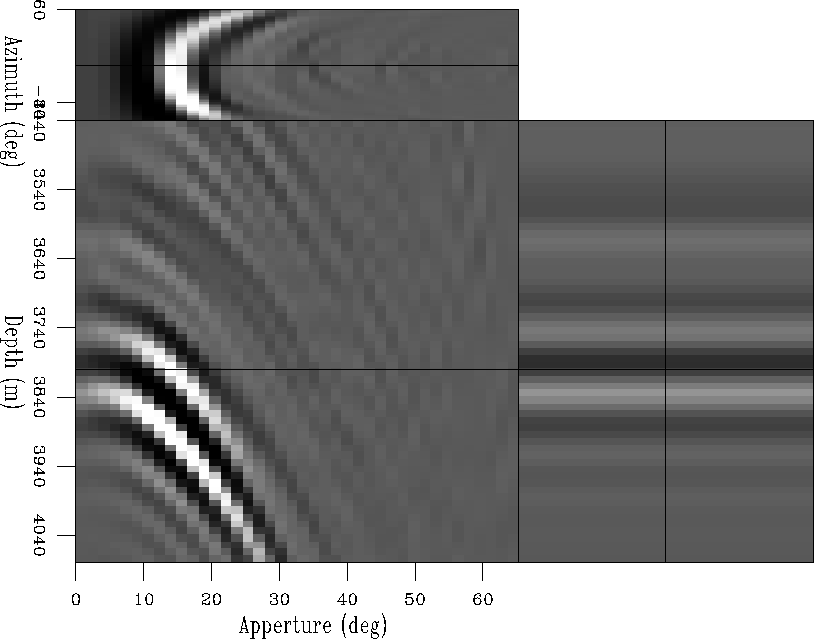
An important issue is to evaluate the degree of azimuth rotation difference between the water-bottom primary and the water-bottom multiple. Because of computational ease, we first windowed the SODCIGs in depth and computed the ADCIGs for the water-bottom primary only. Figure  shows the result for the same ADCIG as in Figure . It is flat for a given azimuth although the range of aperture angles is a function of the azimuth.

Similarly, we windowed the water-bottom multiple and computed the ADCIG as shown in Figure . The depth slice shows a small azimuth rotation when compared with the primary (compare the symmetry of the top panels of Figures  and ).

 

3dadcig1
Figure 16 3D ADCIG at a fixed spatial position for the water-bottom primary.

 

3dadcig2
Figure 17 3D ADCIG at a fixed spatial position for the water-bottom multiple.

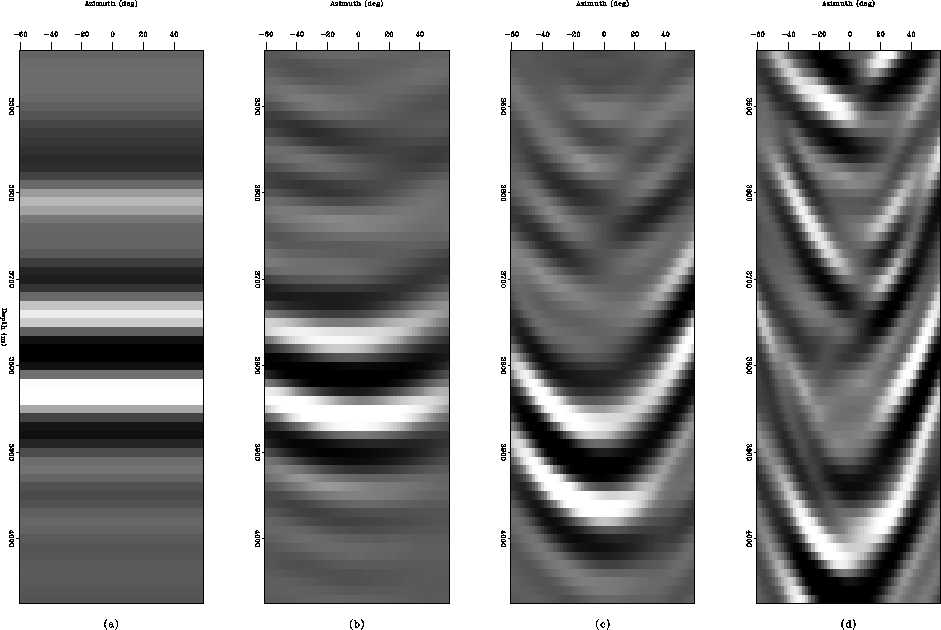
It is interesting to analyze the angle gathers as a function of azimuth for given aperture angles. The water-bottom primary and the water-bottom multiple behave very differently as shown in Figures  and . For the primary, as the aperture angle increases, the angle gather as a function of azimuth loses its flatness and curves down as shown in Biondi (2005). For the multiple, however, as the aperture angle increases the gather as a function of azimuth curves up because it is overmigrated.

 

az_gath1
Figure 18 3D ADCIG for the primary water-bottom reflection as a function of azimuth. The different panels correspond to different aperture angles: (a) 0, (b) 10, (c) 20 and (d) 30 degrees.

 

az_gath2
Figure 19 3D ADCIG for the water-bottom multiple reflection as a function of azimuth. The different panels correspond to different aperture angles: (a) 0, (b) 10, (c) 20 and (d) 30 degrees.