




Next: Parallel implementation
Up: Rosales and Clapp: PS-AMO
Previous: f-k log-stretch PS-AMO
The PS-AMO operator described above works on
a regular sampled cube, our data is recorded on an irregular mesh.
Following the methodology described in Clapp (2006)
we first map our data to a regular 5-D
mesh. For this problem we chose nearest neighbor interpolation,
designated by the operator 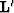 .
For migraion efficiency, and because the five-dimensional space
is sparsely populated, we want to reduce the dimensionality
of our dataset. A common goal, and the one we chose to implement,
was to create common azimuth volume orriented along the inline
direction. As a result we want to eliminate the hy axis.
.
For migraion efficiency, and because the five-dimensional space
is sparsely populated, we want to reduce the dimensionality
of our dataset. A common goal, and the one we chose to implement,
was to create common azimuth volume orriented along the inline
direction. As a result we want to eliminate the hy axis.
Our PS-AMO operator (diagramed in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
allows to transform between various
vector offsets. We use it to transform data from
)
allows to transform between various
vector offsets. We use it to transform data from 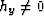 to
hy=0. We can think of it in terms of an operator
to
hy=0. We can think of it in terms of an operator 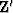 which is a sumation over hy. We can allow for some mixing
between hx by expanding our sumation to form hx=a hy=0,
by summing over all hy and
which is a sumation over hy. We can allow for some mixing
between hx by expanding our sumation to form hx=a hy=0,
by summing over all hy and
| 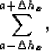 |
(8) |
where 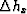 is small.
is small.
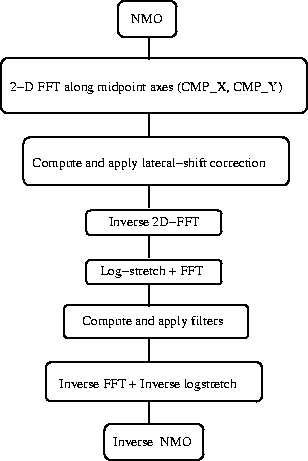
flow
Figure 1 Diagram flow for the
implementation of the PS-AMO operator.
|
|  |

We can combine these two operators to estimate a 4-D model (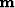 ) from
a 5-D irregular dataset (
) from
a 5-D irregular dataset (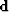 ) through,
) through,
| 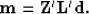 |
(9) |
Equation 9 amounts to just running the adjoint of the inversion
implied by,
| 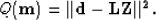 |
(10) |
The adjoint solution is not ideal. The irregularity
of our data can lead to artifical amplitude artifacts.
A solution to this problem is to approximate the
Hessian implied by equation 10 with a diagonal
matrix based on a reference model Rickett (2001),
|  |
(11) |
where
| ![\begin{displaymath}
\bf H = \rm diag \left[ \frac{ \bf Z'\bf L'\bf L\bf Zm_{{\rm ref}}}{{\bf m}_{{\rm ref}}} \right].
\end{displaymath}](img30.gif) |
(12) |
We set our reference model 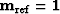 .
.





Next: Parallel implementation
Up: Rosales and Clapp: PS-AMO
Previous: f-k log-stretch PS-AMO
Stanford Exploration Project
4/5/2006
![]() .
For migraion efficiency, and because the five-dimensional space
is sparsely populated, we want to reduce the dimensionality
of our dataset. A common goal, and the one we chose to implement,
was to create common azimuth volume orriented along the inline
direction. As a result we want to eliminate the hy axis.
.
For migraion efficiency, and because the five-dimensional space
is sparsely populated, we want to reduce the dimensionality
of our dataset. A common goal, and the one we chose to implement,
was to create common azimuth volume orriented along the inline
direction. As a result we want to eliminate the hy axis.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
allows to transform between various
vector offsets. We use it to transform data from
)
allows to transform between various
vector offsets. We use it to transform data from ![]() to
hy=0. We can think of it in terms of an operator
to
hy=0. We can think of it in terms of an operator ![]() which is a sumation over hy. We can allow for some mixing
between hx by expanding our sumation to form hx=a hy=0,
by summing over all hy and
which is a sumation over hy. We can allow for some mixing
between hx by expanding our sumation to form hx=a hy=0,
by summing over all hy and

![]() ) from
a 5-D irregular dataset (
) from
a 5-D irregular dataset (![]() ) through,
) through,