f-k log-stretch PS-AMO

The PS-AMO operator is conceived of as a cascade of forward and reverse PS-DMO; therefore, the accuracy and speed of the PS-DMO operator is important. The PS-DMO operator in the frequency-wavenumber domain Alfaraj (1992) is accurate and conceptually simple, but is computationally expensive because the operator is nonstationary in time.

The technique of logarithmic time-stretching, introduced by Bolondi et al. (1982), increases the computational efficiency, because the PP-DMO operator is stationary in the log-stretch domain. Fast Fourier Transforms (FFT) also can be used instead of the slower Discrete Fourier Transforms (DFT). Zhou et al. (1996) create a PP-DMO operator that considers variations of the traveltime as well as variations in the midpoint position before and after PP-DMO; therefore, the operator has the main properties of handling steeply dipping reflectors properly, and producing slightly stronger amplitudes for steep reflectors. Xu et al. (2001) introduce a log-stretch frequency-wavenumber PS-DMO operator that is computationally efficient and kinematically correct; moreover, their implementation performs a correction for the transformation from CMP to CRP. However, this implementation does not consider the variation along CMP as does the PP-DMO Zhou's et al. 1996 PP-DMO operator does. Rosales (2002) follows a procedure similar to the one Zhou et al. (1996) used for the derivation of PP-DMO to create a 3-D PS-DMO operator that that considers both time shift and spatial shift. This 3-D PS-DMO operator is computationally efficient and kinematically correct.

Rosales and Biondi (2002) introduces the PS-AMO operator that we use in this paper. This PS-AMO operator is computationally efficient because it performs in the frequency-wavenumber log-stretch domain. This PS-AMO operator consists of two main operations. In the first operation, the input data ($P(t,{\bf x},{\bf h_1})$) is transformed to the wavenumber domain ($P(t,{\bf k},{\bf h_1})$) using FFT. Then, a lateral-shift correction is applied using the transformation vectors ($\bf D_{10}$ and $\bf D_{02}$) as follows:

 

$$\widetilde P(t,{\bf k},{\bf h_1}) = P(t,{\bf k},{\bf h_1}) e^{i{\bf k}\cdot({\bf D_{10}} - {\bf D_{02}})},$$ (1)

this lateral shift is responsible for the CMP to CRP correction, the transformation vectors, $\bf D_{10}$ and $\bf D_{02}$) are:

$$\begin{eqnarray} {\bf D_{10}}&=&\left[ 1 + \frac{4\gamma \Vert {\bf h_1}\Vert ^2... ... {\bf h_2} \Vert^2}\right] \frac{1-\gamma}{1+\gamma} {\bf h_2}. \end{eqnarray}$$ (2) (3)

The final step of the first operation is to apply a log-stretch along the time axis with the following relation:

 

$$\tau = \ln \left ( \frac{t}{t_c} \right ),$$ (4)

where t_c is the minimum cutoff time, introduced to avoid taking the logarithm of zero. The data set after the first operation is $\widetilde P(\tau,{\bf k},{\bf h_1})$. In the second operation, the log-stretched time domain ($\tau$) section is transformed into the frequency domain ($\Omega$) using FFT. Then, the filters $F(\Omega,{\bf k},{\bf h_1})$ and $F(\Omega,{\bf k},{\bf h_2})$ are applied as follows:

 

$$P(\Omega,{\bf k},{\bf h_2}) = \widetilde P(\Omega,{\bf k},{\... ...c{F(\Omega,{\bf k},{\bf h_1})}{F(\Omega,{\bf k},{\bf h_2})}.$$ (5)

The filter $F(\Omega,{\bf k},{\bf h_i})$ is given by

 

$$F(\Omega,{\bf k},{\bf h_i}) = e^{i\Phi(\Omega,{\bf k},{\bf h_i})},$$ (6)

with the phase function $\Phi(\Omega,{\bf k},{\bf h_i})$ defined by

 

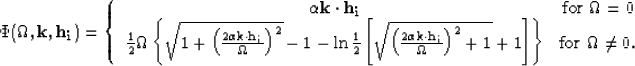$$\Phi(\Omega,{\bf k},{\bf h_i}) = \left \{ \begin{array} {cc}... ...ght \} & \mbox{for $\Omega \ne 0$}. \end{array} \right .$$ (7)

The set of equations 1-7 compose the f-k log-stretch PS-AMO operator. The next session describes the practical implementation of this operator in order to reduce the dimensionality of the data set.