Next: Effects of model regularization
Up: Regularized least-squares inversion
Previous: Regularized Inversion with model
To choose a regularization (39#39)
operator, we must decide what we expect the model to look like. Ideally,
39#39 should be the inverse model covariance (). The
model space generated by my downward-continuation migration method
is a cube with the axes depth (z), common reflection point (CRP), and
offset ray parameter (ph) for a 2-D dataset. For a 3-D dataset,
this model space becomes five dimensional, with axes of z, CRPx, CRPy,
phx and phy. We can expect seismic events to behave in
particular ways along these axes.
Assuming that the correct velocity model was used by the migration
operator, events along the ph axis should be horizontal with
no moveout, as seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . This figure shows the
downward-continuation migration result of a subset of the SMAART JV Sigsbee2A
dataset. The corresponding correct velocity model can be seen in
Figure
. This figure shows the
downward-continuation migration result of a subset of the SMAART JV Sigsbee2A
dataset. The corresponding correct velocity model can be seen in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which is the stratigraphic model that
the velocity models in Figures
, which is the stratigraphic model that
the velocity models in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are based on. Those figures include raytracing to demonstrate the
illumination problems beneath the salt edge, which can be seen as a
decrease in amplitudes in the oval shown in Figure
are based on. Those figures include raytracing to demonstrate the
illumination problems beneath the salt edge, which can be seen as a
decrease in amplitudes in the oval shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In addition to the
expected flat events along ph, we can assume that the reflectivity
(seismic amplitude) along reflection angles should vary smoothly
(, ), and any sudden changes in amplitude are caused
by illumination problems, as explained in the previous chapter and indicated
in Figure
.
In addition to the
expected flat events along ph, we can assume that the reflectivity
(seismic amplitude) along reflection angles should vary smoothly
(, ), and any sudden changes in amplitude are caused
by illumination problems, as explained in the previous chapter and indicated
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by arrows. Since
we believe the model should vary smoothly as a function of angle,
we would expect the amplitude difference as a function of angle to
be small, meaning that we can simply minimize the model styling
goal using a derivative operator as the regularization operator.
This is my geophysical regularization scheme, and is denoted
as 50#50.
by arrows. Since
we believe the model should vary smoothly as a function of angle,
we would expect the amplitude difference as a function of angle to
be small, meaning that we can simply minimize the model styling
goal using a derivative operator as the regularization operator.
This is my geophysical regularization scheme, and is denoted
as 50#50.
zig.mig
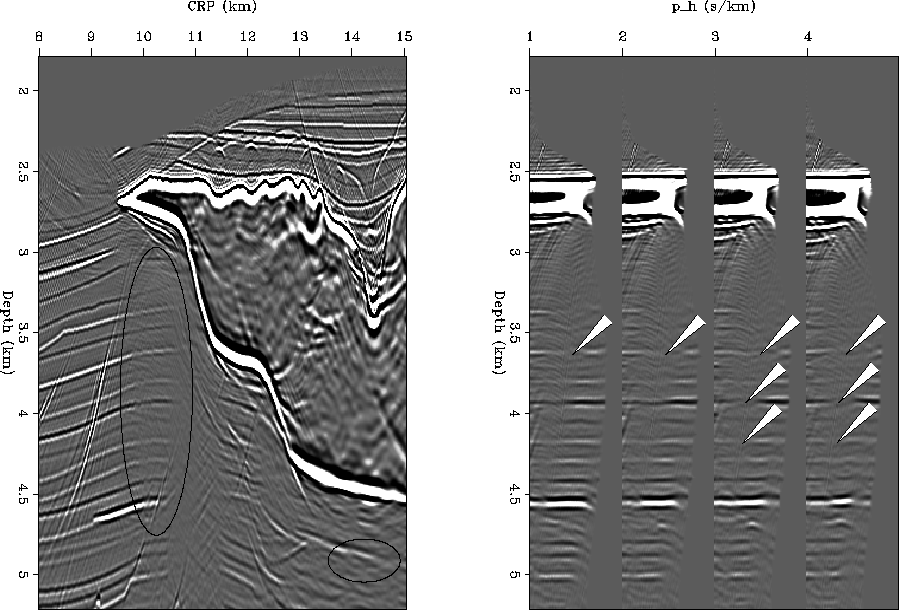
Figure 1 Downward continuation migration
result for part of the Sigsbee2A model. Left: common offset ray parameter
section. Ovals indicate interesting areas of poor illumination.
Right: four CIGs taken from between CRP 10.0 km and 10.25 km. Arrows
indicate holes in the events.




 vel.corvel
vel.corvel
Figure 2 Velocity model for part of the Sigsbee2A model.





We may also have a good idea of the way seismic events should behave
in the CRP-depth plane. An interpreter can pick horizons from a
migration result, and can even extend the horizons into areas of poor
illumination. Alternatively (or additionally), we might have a good
geologic model of the subsurface.
We also know that the amplitudes along the events really
shouldn't decrease suddenly when the reflectors enter a shadow zone
such as that under salt, so we want to minimize this abrupt change.
If we do have an interpretation or geologic model we trust, we should be
able to use this information to regularize the inversion in the
CRP-depth plane. This is my geological regularization scheme, and
is denoted as 51#51.
There are several operators that could be used to implement these
regularization schemes, particularly the geophysical regularization
scheme. One way to regularize the model along the ph axis is
simply to make 50#50 a derivative filter, which is a simple filter
with two coefficients: ``1 52#52''. 53#53 is a number less than or
equal to 1, and helps to control the strength of the regularization.
However, this may not provide a symmetrical effect on the amplitudes.
By applying this filter and its mirror image ``-53#53 1'', a symmetrical
response can be ensured. The result of using this type of filter
for my geophysical regularized inversion with model preconditioning (RIP)
for a part of the Sigsbee2A dataset can be seen in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Note in particular the way the holes along the ph axis are being
filled in (indicated by the arrows) and how much cleaner the shadow zones are.
The amplitudes inside the oval are more consistent. Another possible
50#50 is a steering filter
composed of dip annihilator filters that act horizontally
().
.
Note in particular the way the holes along the ph axis are being
filled in (indicated by the arrows) and how much cleaner the shadow zones are.
The amplitudes inside the oval are more consistent. Another possible
50#50 is a steering filter
composed of dip annihilator filters that act horizontally
().
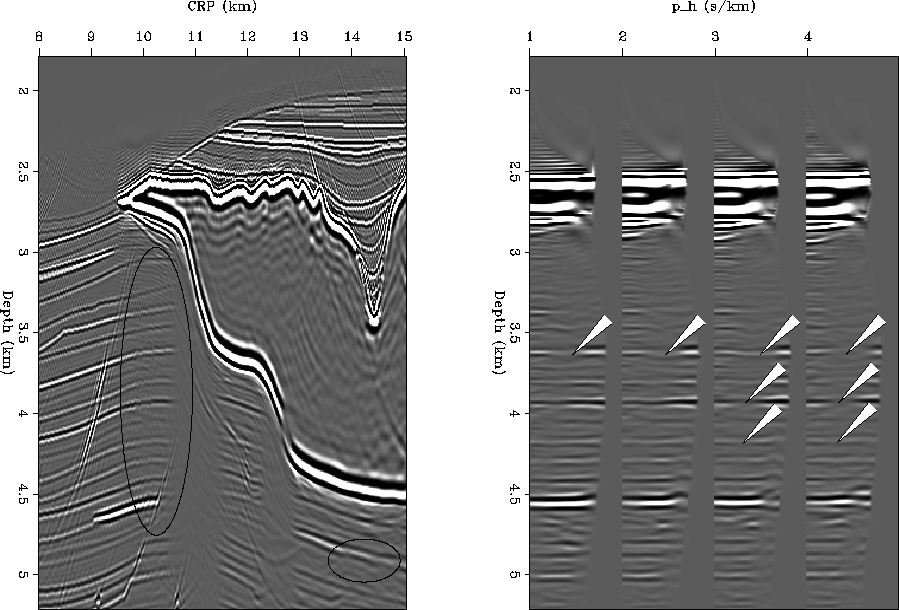
zig.geop.10it
Figure 3 Result of 10 iterations of geophysical
RIP for part of the Sigsbee2A model. Left: common offset ray parameter
section. The amplitudes and continuity within the ovals is improved
compared to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Right: four CIGs taken from between
CRP 10.0 km and 10.25 km. The holes indicated by the arrows are largely
filled in. The artifacts that existed in the shadow zones are cleaned up.
. Right: four CIGs taken from between
CRP 10.0 km and 10.25 km. The holes indicated by the arrows are largely
filled in. The artifacts that existed in the shadow zones are cleaned up.





The versatility of the steering filter allows it to be used in ways
other than just horizontal smoothing along the phx axis. It can
also be used to implement the geological regularization scheme,
meaning that it can act along predetermined dips in the CRP-depth plane.
An interpretation of the structural events can be used to generate
a dip annihilator filter at every model point. All of these individual
dip annihilator filters are then combined together to make the steering filter
itself. This steering filter will then attempt to honor the interpreter's
ideas of what dips should exist, particularly in areas that are in
shadow zones. I choose to combine this with the geophysical regularization,
resulting in a regularization operator 54#54. For simplicity, I
will still refer to this combined regularization operator as geological
regularization.
An example of reflectors picked from the migration result
to be used in constructing a steering filter can be seen in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . For this case, I have not picked reflectors
under the salt. As a result, the dip annihilator filters for each point in
the model beneath the salt will match those at the salt bottom, i.e. the
dips of the sediments beneath the salt are assumed to be similar to the
dip of the salt bottom. The result of geological RIP using these reflectors
on the small
part of the Sigsbee2A dataset is in Figure
. For this case, I have not picked reflectors
under the salt. As a result, the dip annihilator filters for each point in
the model beneath the salt will match those at the salt bottom, i.e. the
dips of the sediments beneath the salt are assumed to be similar to the
dip of the salt bottom. The result of geological RIP using these reflectors
on the small
part of the Sigsbee2A dataset is in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . After
8 iterations, the holes in the CIGs are filled in and the amplitudes of
the reflectors indicated by ovals are more consistent. The area under the
salt shows that where the dip of the salt bottom is low, the dip of the
subsalt sediments is similar and therefore the events are enhanced. Where
the salt bottom has a steep dip, the subsalt sediments do not match that
dip and therefore the events are wiped out - the data do not support the
dips proposed by the model regularization.
. After
8 iterations, the holes in the CIGs are filled in and the amplitudes of
the reflectors indicated by ovals are more consistent. The area under the
salt shows that where the dip of the salt bottom is low, the dip of the
subsalt sediments is similar and therefore the events are enhanced. Where
the salt bottom has a steep dip, the subsalt sediments do not match that
dip and therefore the events are wiped out - the data do not support the
dips proposed by the model regularization.
reflectors
Figure 4 Reflectors picked from the migration
result for part of the Sigsbee2A model, overlaid on the stack of the
migration result.




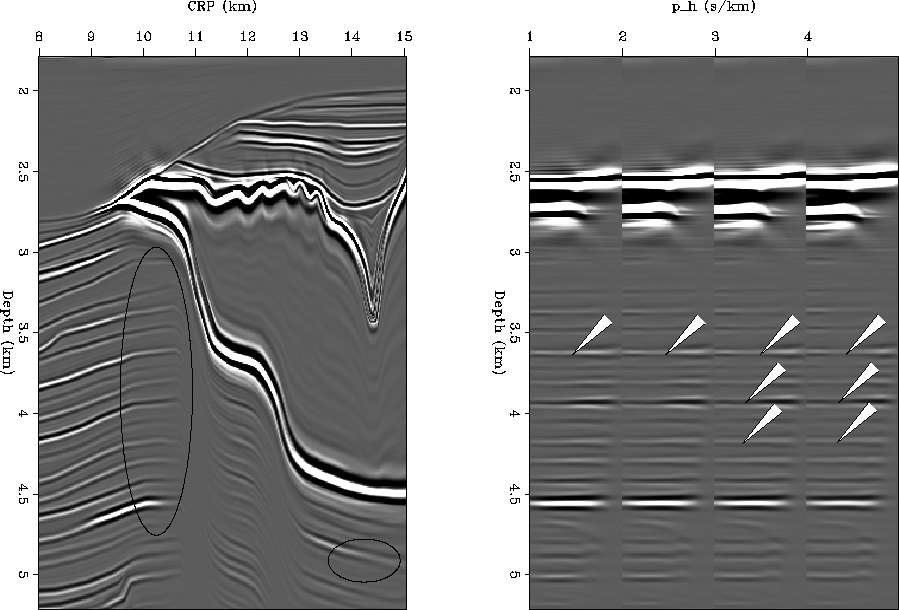
 zig.geol.8it
zig.geol.8it
Figure 5 Result of 8 iterations of geological
RIP for part of the Sigsbee2A model. Left: common offset ray parameter
section. The amplitudes and continuity within the ovals is improved
compared to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Right: four CIGs taken from between CRP 10.0 km and 10.25 km. The holes
indicated by the arrows are completely filled in.
.
Right: four CIGs taken from between CRP 10.0 km and 10.25 km. The holes
indicated by the arrows are completely filled in.





Since this is a synthetic model, we can also pick the exact reflectors
from the reflectivity model. I have overlaid these reflectors on the
migration model in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The result of 8 iterations
of geological RIP using these reflectors can be seen in
Figure
. The result of 8 iterations
of geological RIP using these reflectors can be seen in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Comparing this result with
Figure
. Comparing this result with
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , note in particular the more anticlinal
behavior of the events between CRP = 9.5km and CRP = 12.5km. The
shadow zones are partially filled in, in a reasonable way, as compared
to both the migration result (Fig.
, note in particular the more anticlinal
behavior of the events between CRP = 9.5km and CRP = 12.5km. The
shadow zones are partially filled in, in a reasonable way, as compared
to both the migration result (Fig. ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the geophysical
RIP result (Fig.
) and the geophysical
RIP result (Fig. ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In the common image gathers
(right panels of figures already referred to), both of the geological RIP
results have entirely filled the gaps indicated by the arrows, but the
result using the reflectors from the reflectivity model has improved the
amplitudes of other events as well. It is clear that geological RIP
can improve the image, particularly when the picked reflectors are accurate.
). In the common image gathers
(right panels of figures already referred to), both of the geological RIP
results have entirely filled the gaps indicated by the arrows, but the
result using the reflectors from the reflectivity model has improved the
amplitudes of other events as well. It is clear that geological RIP
can improve the image, particularly when the picked reflectors are accurate.
refsreflect
Figure 6 Reflectors picked from the actual reflectivity
model for part of the Sigsbee2A model, overlaid on the stack of the
migration result.




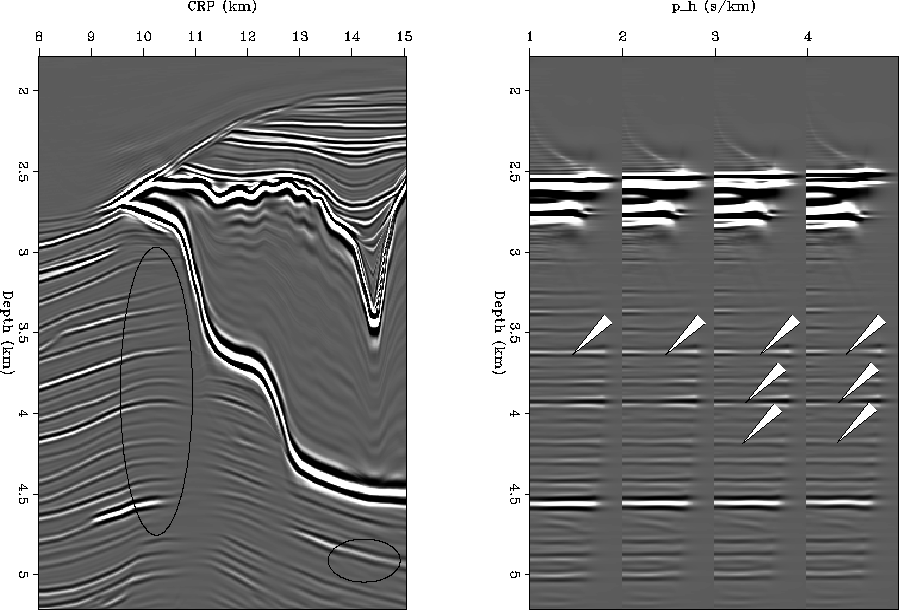
 zig.geolall.8it
zig.geolall.8it
Figure 7 Result of 8 iterations of geological
RIP for part of the Sigsbee2A model, using the reflectors picked from the
actual reflectivity model. Left: common offset ray parameter
section. The amplitudes and continuity within the ovals is improved
compared to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Right: four CIGs taken from between CRP 10.0 km and 10.25 km. The holes
indicated by the arrows are completely filled in.
.
Right: four CIGs taken from between CRP 10.0 km and 10.25 km. The holes
indicated by the arrows are completely filled in.





We also must choose an 40#40. A large 40#40 means that
the regularization will be strong (we will be enforcing our idea of
the model more) and
a small 40#40 means the regularization is not strong (we rely on
the data more). Choosing a balanced 40#40 will help to fill the
null space in a reasonable way.





Next: Effects of model regularization
Up: Regularized least-squares inversion
Previous: Regularized Inversion with model
Stanford Exploration Project
10/31/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . This figure shows the
downward-continuation migration result of a subset of the SMAART JV Sigsbee2A
dataset. The corresponding correct velocity model can be seen in
Figure
. This figure shows the
downward-continuation migration result of a subset of the SMAART JV Sigsbee2A
dataset. The corresponding correct velocity model can be seen in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which is the stratigraphic model that
the velocity models in Figures
, which is the stratigraphic model that
the velocity models in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are based on. Those figures include raytracing to demonstrate the
illumination problems beneath the salt edge, which can be seen as a
decrease in amplitudes in the oval shown in Figure
are based on. Those figures include raytracing to demonstrate the
illumination problems beneath the salt edge, which can be seen as a
decrease in amplitudes in the oval shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In addition to the
expected flat events along ph, we can assume that the reflectivity
(seismic amplitude) along reflection angles should vary smoothly
(, ), and any sudden changes in amplitude are caused
by illumination problems, as explained in the previous chapter and indicated
in Figure
.
In addition to the
expected flat events along ph, we can assume that the reflectivity
(seismic amplitude) along reflection angles should vary smoothly
(, ), and any sudden changes in amplitude are caused
by illumination problems, as explained in the previous chapter and indicated
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by arrows. Since
we believe the model should vary smoothly as a function of angle,
we would expect the amplitude difference as a function of angle to
be small, meaning that we can simply minimize the model styling
goal using a derivative operator as the regularization operator.
This is my geophysical regularization scheme, and is denoted
as 50#50.
by arrows. Since
we believe the model should vary smoothly as a function of angle,
we would expect the amplitude difference as a function of angle to
be small, meaning that we can simply minimize the model styling
goal using a derivative operator as the regularization operator.
This is my geophysical regularization scheme, and is denoted
as 50#50.