




Next: Signal and noise PEFs
Up: Multiple attenuation: Theory and
Previous: Introduction
The key assumption of the proposed multiple attenuation technique is that
primaries and multiples have different multidimensional
spectra that PEFs can approximate Claerbout (1992); Spitz (1999).
These filters can be interpreted as multidimensional dip filters.
The estimation of these filters is based on the spatial predictability
of seismic events. Therefore, PEFs for primaries and multiples are
needed prior to the subtraction step.
This section describes how these filters are estimated.
The PEFs used here are time-space domain non-stationary
filters to cope with the variability of seismic data
with time, offset and shot position. Implementing non-stationary
filters is not an easy task. A possible solution is to break-up
the dataset into patches and estimate a filter for each patch.
However, reassembling these patches create edge effects in the
overlapping zones. Alternatively, non-stationary
convolution or combination can be used to estimate one filter
per data point Margrave (1998) or more realistically,
per micro-patch Crawley (2000). A micro-patch is made of
a succession of data points that share the same filter.
With this technique, the filters can vary smoothly across the dataset
while leaving almost no edge effect.
A detailed description of the non-stationary filters is given
in Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Here I present
the most important steps of the filter estimation procedure only.
Calling
. Here I present
the most important steps of the filter estimation procedure only.
Calling 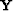 the non-stationary combination matrix
Margrave (1998) with the data vector
the non-stationary combination matrix
Margrave (1998) with the data vector 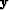 from which we
want to estimate the filters and
from which we
want to estimate the filters and  the unknown PEFs
coefficients, one way to estimate the PEFs is to minimize the
length of residual vectors
the unknown PEFs
coefficients, one way to estimate the PEFs is to minimize the
length of residual vectors 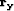 Claerbout and Fomel (2002):
Claerbout and Fomel (2002):
| 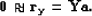 |
(45) |
This last expression is also called fitting goal.
By definition of the PEFs, the first coefficient is always one
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
To take this requirement into account, equation (
).
To take this requirement into account, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
becomes
)
becomes
| 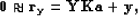 |
(46) |
where 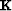 is a masking operator that forces the first coefficient
of the PEFs to be one.
is a masking operator that forces the first coefficient
of the PEFs to be one.
If one filter is used per data point, the matrix
of unknown coefficients  can be enormous, making the problem
very underdetermined. This difficulty can be overcome in two ways.
Firstly, the filter is kept constant inside a micro-patch. Secondly,
a smoothing operator
can be enormous, making the problem
very underdetermined. This difficulty can be overcome in two ways.
Firstly, the filter is kept constant inside a micro-patch. Secondly,
a smoothing operator 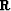 is introduced to penalize strong
variations between neighboring filters. Both strategies are considered here.
Introducing the Laplacian operator
is introduced to penalize strong
variations between neighboring filters. Both strategies are considered here.
Introducing the Laplacian operator 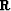 , equation
(
, equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is augmented as follows:
) is augmented as follows:
| 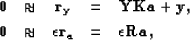 |
(47) |
where  is a trade-off parameter between coefficient
estimation and filter smoothing. The Laplacian operator smoothes along
two (i.e., time/offset) or three axes (i.e., time/offset/shot)
depending on the PEF's dimensions.
A least-squares estimate of the PEF's coefficients leads
to the following objective function:
is a trade-off parameter between coefficient
estimation and filter smoothing. The Laplacian operator smoothes along
two (i.e., time/offset) or three axes (i.e., time/offset/shot)
depending on the PEF's dimensions.
A least-squares estimate of the PEF's coefficients leads
to the following objective function:
| 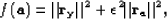 |
(48) |
where  is estimated iteratively with the conjugate-gradient
method and
is estimated iteratively with the conjugate-gradient
method and  is chosen by trial and error. Note that the
Huber norm of Chapter
is chosen by trial and error. Note that the
Huber norm of Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is not used here.
is not used here.
The amplitudes of seismic data vary across offset, shot and
time. Large amplitude variations can be troublesome with
least-squares inversion because they tend to bias the final result
Claerbout (1992) by ignoring or over-fitting some areas of the data.
Therefore, it is important to make sure that these amplitude
variations do not affect our processing. One solution is to apply a
weight to the data prior to the inversion
like Automatic Gain Control (AGC) or a geometrical
spreading correction. Alternatively, a weight 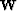 can be incorporated
inside the fitting goals in equation (
can be incorporated
inside the fitting goals in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| 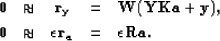 |
(49) |
This weight can be interpreted as a change of norm consistent with the
data, similar to  norm.
In this Chapter,
norm.
In this Chapter, 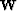 is obtained by computing for each shot gather
is obtained by computing for each shot gather
| 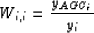 |
(50) |
where 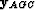 is the data vector with AGC applied. If division
by zero occurs, the weight is set to zero.
This weight can also incorporate a mute zone where no data are present.
Thanks to the helical boundary conditions
Claerbout (1998); Mersereau and Dudgeon (1974),
the PEFs can have any dimension. In this Chapter, I use 2-D
(time/offset) and 3-D (time/offset/shot position)
pef
is the data vector with AGC applied. If division
by zero occurs, the weight is set to zero.
This weight can also incorporate a mute zone where no data are present.
Thanks to the helical boundary conditions
Claerbout (1998); Mersereau and Dudgeon (1974),
the PEFs can have any dimension. In this Chapter, I use 2-D
(time/offset) and 3-D (time/offset/shot position)
pef
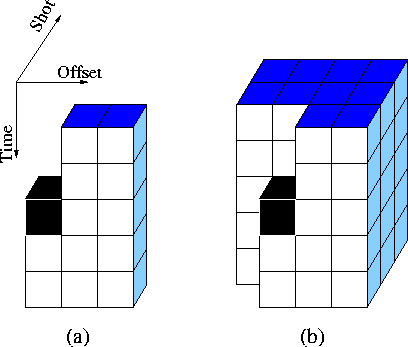
Figure 1 prediction-error filters in (a) 2-D and (b) 3-D.
The first coefficient in black is always one.

filters (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and demonstrate that 3-D filters lead to the best noise attenuation
results. When 2-D filters are used, the multiple attenuation is
performed on one shot gather at a time. When 3-D filters are used,
the multiple attenuation is performed on one macro-gather at a
time. A macro-gather is a cube made of adjacent shots
with all the offsets and time samples. There is an overlapping zone of
five shot gathers between neighboring macro-patches. When the multiple attenuation
is done, the macro-gathers are reassembled to form the final result.
The next section describes how to choose the model
) and demonstrate that 3-D filters lead to the best noise attenuation
results. When 2-D filters are used, the multiple attenuation is
performed on one shot gather at a time. When 3-D filters are used,
the multiple attenuation is performed on one macro-gather at a
time. A macro-gather is a cube made of adjacent shots
with all the offsets and time samples. There is an overlapping zone of
five shot gathers between neighboring macro-patches. When the multiple attenuation
is done, the macro-gathers are reassembled to form the final result.
The next section describes how to choose the model 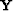 in equation
(
in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) when PEFs for multiples and primaries are estimated.
) when PEFs for multiples and primaries are estimated.





Next: Signal and noise PEFs
Up: Multiple attenuation: Theory and
Previous: Introduction
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Here I present
the most important steps of the filter estimation procedure only.
Calling
. Here I present
the most important steps of the filter estimation procedure only.
Calling ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Here I present
the most important steps of the filter estimation procedure only.
Calling
. Here I present
the most important steps of the filter estimation procedure only.
Calling ![]() the non-stationary combination matrix
Margrave (1998) with the data vector
the non-stationary combination matrix
Margrave (1998) with the data vector ![]() from which we
want to estimate the filters and
from which we
want to estimate the filters and ![]() the unknown PEFs
coefficients, one way to estimate the PEFs is to minimize the
length of residual vectors
the unknown PEFs
coefficients, one way to estimate the PEFs is to minimize the
length of residual vectors ![]() Claerbout and Fomel (2002):
Claerbout and Fomel (2002):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
To take this requirement into account, equation (
).
To take this requirement into account, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
becomes
)
becomes
![]() can be enormous, making the problem
very underdetermined. This difficulty can be overcome in two ways.
Firstly, the filter is kept constant inside a micro-patch. Secondly,
a smoothing operator
can be enormous, making the problem
very underdetermined. This difficulty can be overcome in two ways.
Firstly, the filter is kept constant inside a micro-patch. Secondly,
a smoothing operator ![]() is introduced to penalize strong
variations between neighboring filters. Both strategies are considered here.
Introducing the Laplacian operator
is introduced to penalize strong
variations between neighboring filters. Both strategies are considered here.
Introducing the Laplacian operator ![]() , equation
(
, equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is augmented as follows:
) is augmented as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is not used here.
is not used here.
![]() can be incorporated
inside the fitting goals in equation (
can be incorporated
inside the fitting goals in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and demonstrate that 3-D filters lead to the best noise attenuation
results. When 2-D filters are used, the multiple attenuation is
performed on one shot gather at a time. When 3-D filters are used,
the multiple attenuation is performed on one macro-gather at a
time. A macro-gather is a cube made of adjacent shots
with all the offsets and time samples. There is an overlapping zone of
five shot gathers between neighboring macro-patches. When the multiple attenuation
is done, the macro-gathers are reassembled to form the final result.
The next section describes how to choose the model
) and demonstrate that 3-D filters lead to the best noise attenuation
results. When 2-D filters are used, the multiple attenuation is
performed on one shot gather at a time. When 3-D filters are used,
the multiple attenuation is performed on one macro-gather at a
time. A macro-gather is a cube made of adjacent shots
with all the offsets and time samples. There is an overlapping zone of
five shot gathers between neighboring macro-patches. When the multiple attenuation
is done, the macro-gathers are reassembled to form the final result.
The next section describes how to choose the model ![]() in equation
(
in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) when PEFs for multiples and primaries are estimated.
) when PEFs for multiples and primaries are estimated.