




Next: Adaptive subtraction results
Up: 2-D data example: attenuation
Previous: The synthetic data
To handle the inherent non-stationarity of seismic data, I estimate
a bank of non-stationary filters using helical boundary
conditions Claerbout (1998); Mersereau and Dudgeon (1974). This approach has been successfully
utilized by Rickett et al. (2001) to attenuate surface-related multiples.
As described before [equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )],
I use the Huber norm to approximate the
)],
I use the Huber norm to approximate the  norm and a standard conjugate-gradient
solver with the
norm and a standard conjugate-gradient
solver with the  norm. The filter coefficients vary smoothly
across the output space by introducing a regularization term inside
equation (
norm. The filter coefficients vary smoothly
across the output space by introducing a regularization term inside
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) Crawley (2000); Rickett et al. (2001).
The misfit function to minimize becomes
) Crawley (2000); Rickett et al. (2001).
The misfit function to minimize becomes
|  |
(13) |
interl2
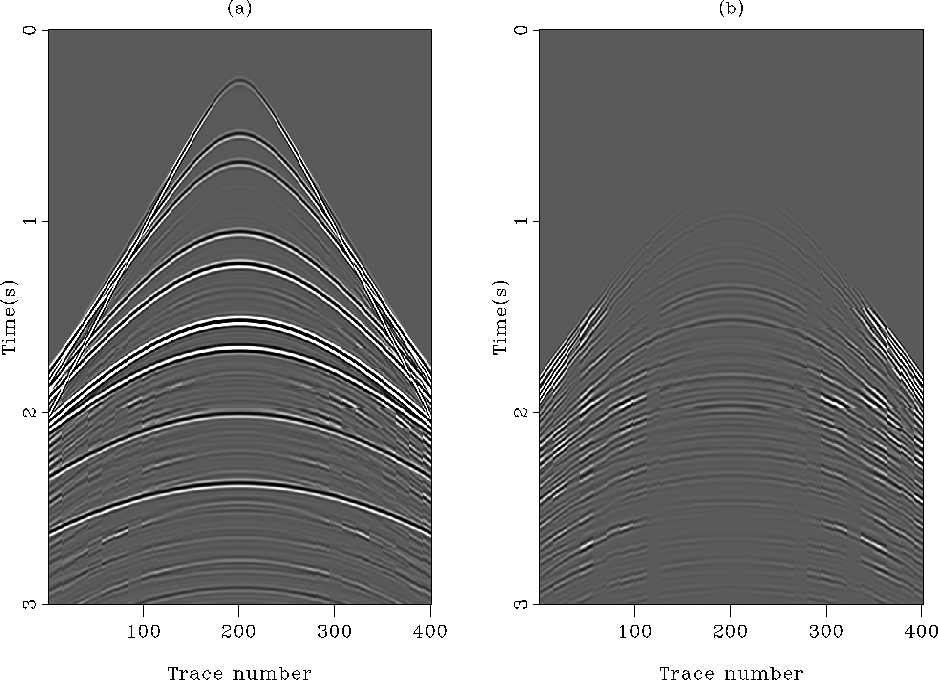
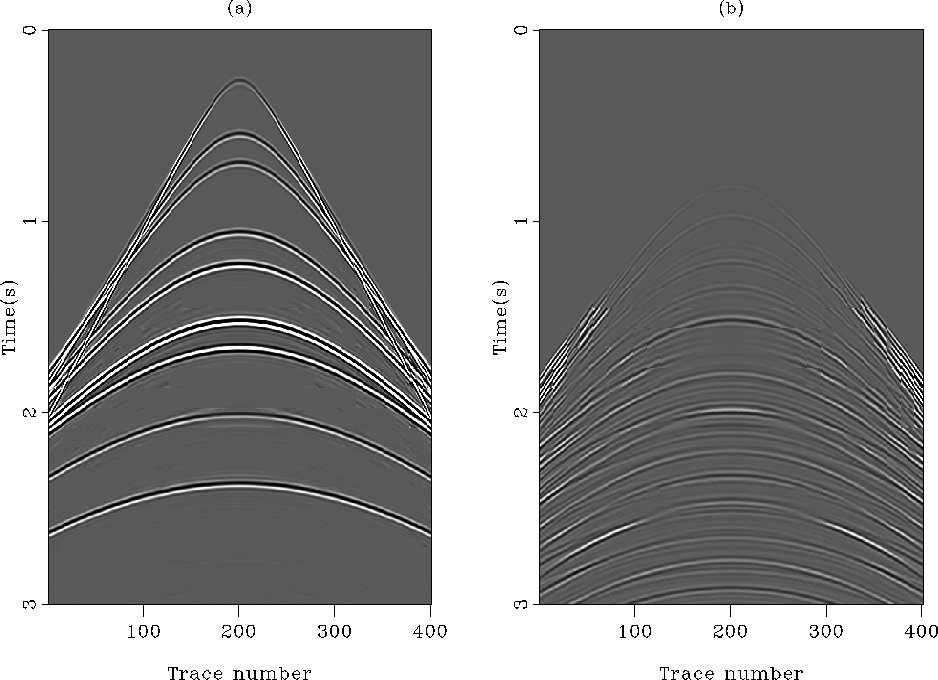
Figure 7 (a) The estimated primaries
with the  norm. (b) The estimated internal multiples with the
norm. (b) The estimated internal multiples with the
 norm. Ideally, (b) should look like Figure
norm. Ideally, (b) should look like Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b,
but it does not.
b,
but it does not.




 interl1
interl1
Figure 8 (a) The estimated primaries
with the  norm. (b) The estimated internal multiples with the
norm. (b) The estimated internal multiples with the
 norm. Beside some edge-effects, (b) resembles
closely Figure
norm. Beside some edge-effects, (b) resembles
closely Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. The adaptive subtraction worked
very well.
b. The adaptive subtraction worked
very well.





where 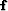 is the unknown vector of filter coefficients for the
non-stationary matching filters and
is the unknown vector of filter coefficients for the
non-stationary matching filters and 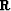 is a regularization
operator. The Helix derivative Claerbout (1998) is chosen for
is a regularization
operator. The Helix derivative Claerbout (1998) is chosen for 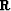 .In the following results, the non-stationary filters
are 1-D. The same number of coefficients per filter are estimated with
both
.In the following results, the non-stationary filters
are 1-D. The same number of coefficients per filter are estimated with
both  and
and  norms.
norms.





Next: Adaptive subtraction results
Up: 2-D data example: attenuation
Previous: The synthetic data
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )],
I use the Huber norm to approximate the
)],
I use the Huber norm to approximate the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) Crawley (2000); Rickett et al. (2001).
The misfit function to minimize becomes
) Crawley (2000); Rickett et al. (2001).
The misfit function to minimize becomes
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b,
but it does not.
b,
but it does not.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. The adaptive subtraction worked
very well.
b. The adaptive subtraction worked
very well.
![]() is the unknown vector of filter coefficients for the
non-stationary matching filters and
is the unknown vector of filter coefficients for the
non-stationary matching filters and ![]() is a regularization
operator. The Helix derivative Claerbout (1998) is chosen for
is a regularization
operator. The Helix derivative Claerbout (1998) is chosen for ![]() .In the following results, the non-stationary filters
are 1-D. The same number of coefficients per filter are estimated with
both
.In the following results, the non-stationary filters
are 1-D. The same number of coefficients per filter are estimated with
both ![]() and
and ![]() norms.
norms.