




Next: Results on a simple
Up: Principles of norm and
Previous: Shaping filters and the
The strong primary in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) can be seen as an outlier
that attracts much of the solver's efforts during the filter estimation.
can be seen as an outlier
that attracts much of the solver's efforts during the filter estimation.
filterl2
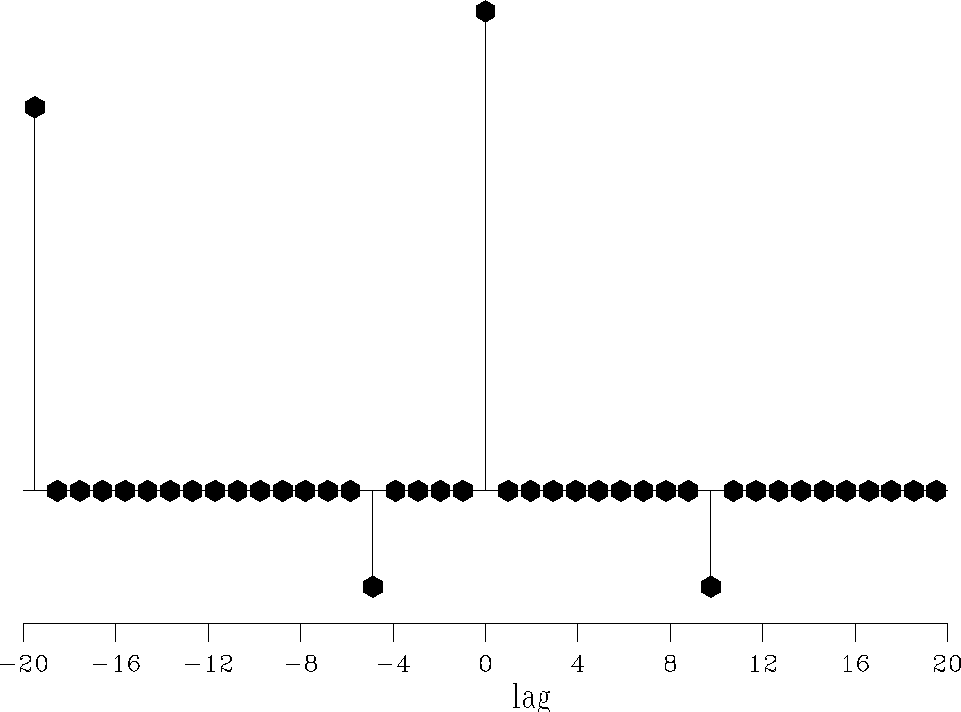
Figure 3 Shaping filter estimated for the
1-D problem with the  norm. This filter is not a single
spike at lag=0. norm. This filter is not a single
spike at lag=0.
|
|  |





filterl1
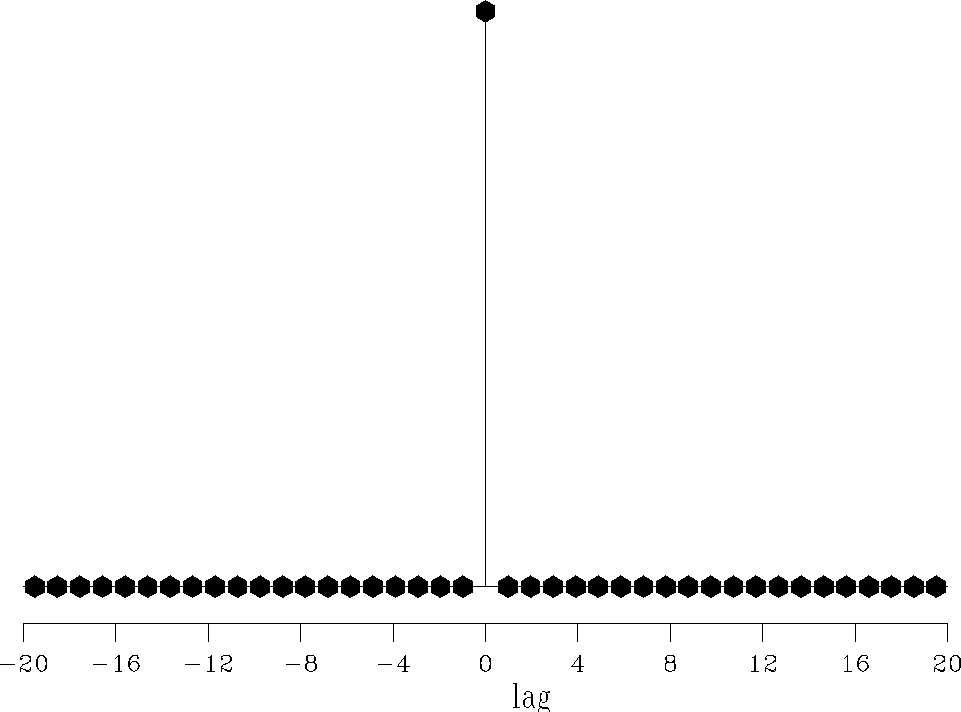
Figure 4 Shaping filter estimated for the
1-D problem with the  norm. This filter is a single spike at
lag=0. norm. This filter is a single spike at
lag=0.
|
|  |





Consequently, some of the signal leaks into the
noise. Because the  norm is robust to outliers, I propose
estimating the filter coefficients with it. This insensitivity to large
``noise'' has a statistical interpretation: robust measures are
related to long-tailed density functions in the same way that
norm is robust to outliers, I propose
estimating the filter coefficients with it. This insensitivity to large
``noise'' has a statistical interpretation: robust measures are
related to long-tailed density functions in the same way that  is related to the short-tailed gaussian density function Tarantola (1987).
In this section, I show that the
is related to the short-tailed gaussian density function Tarantola (1987).
In this section, I show that the  norm solves the problem
highlighted in the preceding section.
norm solves the problem
highlighted in the preceding section.
Now our goal is to estimate one shaping filter 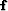 that minimizes
the objective function
that minimizes
the objective function
| 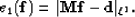 |
(10) |
The function in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is singular where any residual
component vanishes implying that the derivative of
) is singular where any residual
component vanishes implying that the derivative of 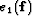 is not
continuous everywhere. Unfortunately, most of our optimization
techniques, e.g., conjugate-gradient or Newton methods,
assume that the first derivative of the objective function is
continuous in order to find its minimum. Therefore, specialized
techniques have been developed to either minimize or approximate the
is not
continuous everywhere. Unfortunately, most of our optimization
techniques, e.g., conjugate-gradient or Newton methods,
assume that the first derivative of the objective function is
continuous in order to find its minimum. Therefore, specialized
techniques have been developed to either minimize or approximate the
 norm.
For instance, various approaches based on a linear programming viewpoint have been used
with success, e.g., Barrodale and Roberts
1980.
Another idea is to minimize a hybrid
norm.
For instance, various approaches based on a linear programming viewpoint have been used
with success, e.g., Barrodale and Roberts
1980.
Another idea is to minimize a hybrid 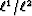 norm
with an iteratively reweighted least-squares (IRLS) method
Bube and Langan (1997); Gersztenkorn et al. (1986); Scales and Gersztenkorn (1988).
norm
with an iteratively reweighted least-squares (IRLS) method
Bube and Langan (1997); Gersztenkorn et al. (1986); Scales and Gersztenkorn (1988).
Alternatively, the Huber norm is utilized.
This technique yields a good approximation of the  norm.
Therefore, the objective function we minimize becomes
norm.
Therefore, the objective function we minimize becomes
| 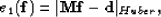 |
(11) |
The minimization of the Huber norm is performed with a quasi-Newton
method (Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The only parameter that
needs to be set is
). The only parameter that
needs to be set is  in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Consistent with
the strategy of Chapter
). Consistent with
the strategy of Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I set
, I set
| 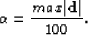 |
(12) |
From now on, I call  norm the Huber norm. In text section, I
show that the
norm the Huber norm. In text section, I
show that the  norm leads to the desired result for
the filter estimation problem.
norm leads to the desired result for
the filter estimation problem.





Next: Results on a simple
Up: Principles of norm and
Previous: Shaping filters and the
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) can be seen as an outlier
that attracts much of the solver's efforts during the filter estimation.
can be seen as an outlier
that attracts much of the solver's efforts during the filter estimation.


![]() norm is robust to outliers, I propose
estimating the filter coefficients with it. This insensitivity to large
``noise'' has a statistical interpretation: robust measures are
related to long-tailed density functions in the same way that
norm is robust to outliers, I propose
estimating the filter coefficients with it. This insensitivity to large
``noise'' has a statistical interpretation: robust measures are
related to long-tailed density functions in the same way that ![]() is related to the short-tailed gaussian density function Tarantola (1987).
In this section, I show that the
is related to the short-tailed gaussian density function Tarantola (1987).
In this section, I show that the ![]() norm solves the problem
highlighted in the preceding section.
norm solves the problem
highlighted in the preceding section.
![]() that minimizes
the objective function
that minimizes
the objective function
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is singular where any residual
component vanishes implying that the derivative of
) is singular where any residual
component vanishes implying that the derivative of ![]() norm.
Therefore, the objective function we minimize becomes
norm.
Therefore, the objective function we minimize becomes
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The only parameter that
needs to be set is
). The only parameter that
needs to be set is ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Consistent with
the strategy of Chapter
). Consistent with
the strategy of Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I set
, I set