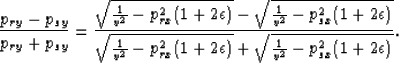Stationary path and the constraints on the ray directions

In this section we show that the stationary path approximation derived in the previous section (equation (9)) is equivalent to imposing the constraint that the source and receiver rays must be coplanar. For this constraint to hold, the following relation must be satisfied among the ray parameters:  

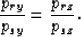$$\frac{p_{ry}}{p_{sy}} = \frac{p_{rz}}{p_{sz}}.$$ (11)

where (p_sx, p_sy,p_sz) are the rays downward propagating the sources and (p_rx, p_ry,p_rz) are the rays downward propagating the receivers. Applying the transformation from wavenumbers to ray parameter using the relation 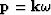$\bold p = \bold k\omega$ to equation (3) we have:  

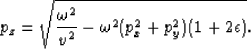$$p_z = \sqrt{\frac{\omega^2}{v^2} - \omega^2(p_x^2 + p_y^2) (1 + 2\epsilon)}.$$ (12)

Substituting equation (12) in equation (11) and after some algebra we get:  

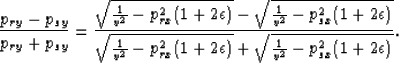$$\frac{p_{ry} - p_{sy}}{p_{ry} + p_{sy}} = \frac{\sqrt{\frac{... ... 2\epsilon)} + \sqrt{\frac{1}{v^2} - p_{sx}^2(1 + 2\epsilon)}}.$$ (13)

Substituting the following relations in equation(13) gives the stationary path approximation derived in the previous section given by equation (9):  

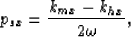$$p_{sx} = \frac{k_{mx} - k_{hx}}{2\omega},$$ (14)

 

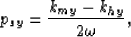$$p_{sy} = \frac{k_{my} - k_{hy}}{2\omega},$$ (15)

 

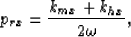$$p_{rx} = \frac{k_{mx} + k_{hx}}{2\omega},$$ (16)

 

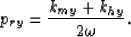$$p_{ry} = \frac{k_{my} + k_{hy}}{2\omega}.$$ (17)