




Next: Appendix B: Hill's Equation
Up: Berryman: Geomechanical constants of
Previous: CONCLUSIONS
Although Eq. (20) for the overall volume effective stress coefficient
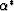 is known to be true for homogeneous pore saturation,
we also need to have a corresponding result here for patchy
saturation.
It turns out that the same formula applies for arbitrarily patchy
saturated media, as long as there are only two types of solid components.
To show this, consider
is known to be true for homogeneous pore saturation,
we also need to have a corresponding result here for patchy
saturation.
It turns out that the same formula applies for arbitrarily patchy
saturated media, as long as there are only two types of solid components.
To show this, consider
| 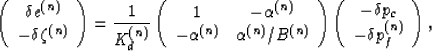 |
(26) |
where 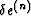 and
and 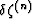 are the change in
overall strain
and the increment of fluid content in component n, where n = 1,2.
[There are also similar formulas for all the overall properties with
(n) replaced by * for the corresponding effective properties.
See Berryman and Wang (1995) for more discussion.]
Similarly, the change in overall confining (external) pressure is
are the change in
overall strain
and the increment of fluid content in component n, where n = 1,2.
[There are also similar formulas for all the overall properties with
(n) replaced by * for the corresponding effective properties.
See Berryman and Wang (1995) for more discussion.]
Similarly, the change in overall confining (external) pressure is
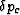 , and the pore pressure change of component n is
, and the pore pressure change of component n is
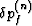 .The porous material coefficients are defined as in the main text,
Kd(n) is the drained bulk modulus,
.The porous material coefficients are defined as in the main text,
Kd(n) is the drained bulk modulus, 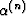 is the volume
effective stress coefficient, and B(n) is Skempton's coefficient
for the n-th constituent.
is the volume
effective stress coefficient, and B(n) is Skempton's coefficient
for the n-th constituent.
Now the rest of the argument follows that given in Berryman and Milton
(1991) exactly, since it is not important what fluid is in the pores when
trying to determine the overall effective stress coefficient
at long times (when fluid pressure in the system has equilibrated).
We simply postulate the existence of any fixed ratio
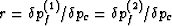 such that
such that 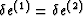 . If there is such a ratio (valid at
appropriately long times), then
. If there is such a ratio (valid at
appropriately long times), then
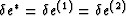 also follows immediately and we have the condition that must be satisfied:
also follows immediately and we have the condition that must be satisfied:
| ![\begin{displaymath}
\frac{\delta p_c}{K_d^{(1)}}\left[1-\alpha^{(1)}r\right] =
\frac{\delta p_c}{K_d^{(2)}}\left[1-\alpha^{(2)}r\right],
\end{displaymath}](img101.gif) |
(27) |
which is just a linear relation for ratio r. The result shows that
the postulated value of r does exist unless the denominator
of the following expression vanishes:
| 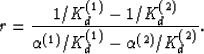 |
(28) |
If the numerator of (28) vanishes, the results are trivial
because Gassmann's microhomogeneity condition is then satisfied.
Once the value of r is known, it is easy to see that
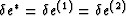 implies
implies
| ![\begin{displaymath}
\frac{\delta p_c}{K_d^*}\left[1-\alpha^*r\right] =
\frac{\delta p_c}{K_d^{(1)}}\left[1-\alpha^{(1)}r\right].
\end{displaymath}](img103.gif) |
(29) |
This equation can be rearranged into the form (20), as
has been shown previously by Berryman and Milton (1991).
Arguments similar to the one just given have also been used,
for example, in the context of thermal expansion by Benveniste and Dvorak
(1990) and Dvorak and Benveniste (1997),
who call this
approach ``the theory of uniform fields.'' It turns out this method is
not restricted to isotropic constituents as one might infer from the
arguments presented here and also in (Berryman and Milton, 1991).
A somewhat more difficult task than the one just accomplished involves
deducing the overall effective pore bulk modulus 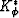 as was
also done previously by Berryman and Milton (1991).
However, this coefficient
does not play any direct role in our present analysis, so we will
leave this exercise to the interested reader.
as was
also done previously by Berryman and Milton (1991).
However, this coefficient
does not play any direct role in our present analysis, so we will
leave this exercise to the interested reader.





Next: Appendix B: Hill's Equation
Up: Berryman: Geomechanical constants of
Previous: CONCLUSIONS
Stanford Exploration Project
5/3/2005
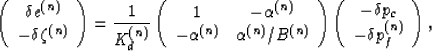
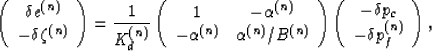
![]() such that
such that ![]() . If there is such a ratio (valid at
appropriately long times), then
. If there is such a ratio (valid at
appropriately long times), then
![]() also follows immediately and we have the condition that must be satisfied:
also follows immediately and we have the condition that must be satisfied:
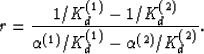
![]() as was
also done previously by Berryman and Milton (1991).
However, this coefficient
does not play any direct role in our present analysis, so we will
leave this exercise to the interested reader.
as was
also done previously by Berryman and Milton (1991).
However, this coefficient
does not play any direct role in our present analysis, so we will
leave this exercise to the interested reader.