




Next: Formation factor bounds
Up: CONDUCTIVITY: CANONICAL FUNCTIONS AND
Previous: Comparisons of conductivity bounds
There are other methods for conductivity/permittivity analysis.
The Bergman-Milton
(Bergman, 1978; 1980; 1982; Milton, 1980; 1981; Korringa and
LaTorraca, 1986; Stroud et al., 1986; Berryman, 1992)
analytical approach to understanding some general effective transport
coefficient or permittivity -- which we take for example to be 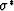 --
of two-component inhomogeneous media shows that
--
of two-component inhomogeneous media shows that
| 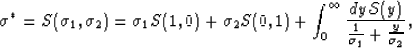 |
(40) |
where S(1,0) and S(0,1) are constants depending only on the
geometry and 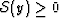 is a resonance density functional
also depending only on the geometry. The integral in
(40) is known as a Stieltjes integral (Baker, 1975).
This formula is typically derived and used for the
case of complex constants:
is a resonance density functional
also depending only on the geometry. The integral in
(40) is known as a Stieltjes integral (Baker, 1975).
This formula is typically derived and used for the
case of complex constants: 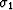 ,
, 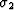 , and
, and 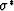 .But we will restrict consideration here - as
Bergman (1978) did in his early work - to pure
conductors so that
.But we will restrict consideration here - as
Bergman (1978) did in his early work - to pure
conductors so that 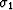 ,
, 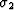 , and
, and 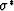 are all real and
nonnegative.
are all real and
nonnegative.
A short derivation of (40) is instructive, so we
will present one now.
Following (for example) Korringa and LaTorraca (1986) we consider the defining equation for the function Z(s)
| 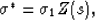 |
(41) |
where
| 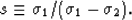 |
(42) |
Then, Milton (1981) shows [also see Korringa and LaTorraca, 1986] that
| 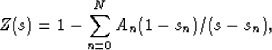 |
(43) |
where the sn's are the locations of the poles, and are enumerated in
increasing order. The An's are the residues. These real constants
satisfy the following inequalties: 0 < An < 1,
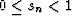 , and
, and 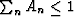 . Note that N might be a
very large number in practice, so that it may then be more convenient
to think of turning this sum into an integral. Define a density functional
. Note that N might be a
very large number in practice, so that it may then be more convenient
to think of turning this sum into an integral. Define a density functional
| 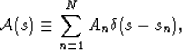 |
(44) |
where 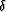 is the Dirac delta function. Then, (43) can be
rewitten as
is the Dirac delta function. Then, (43) can be
rewitten as
| 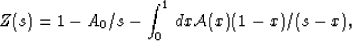 |
(45) |
which is so far just a restatement of (43), assuming only
that there exists a finite A0 for which 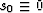 . Substituting
(42) into (45) and rearranging, we find
. Substituting
(42) into (45) and rearranging, we find
| 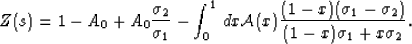 |
(46) |
We can then symmetrize this expression by adding and subtracting the
term 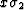 in the numerator of the displayed ratio inside the
integral. Then we can pull out another constant and finally have
the form we want:
in the numerator of the displayed ratio inside the
integral. Then we can pull out another constant and finally have
the form we want:
| ![\begin{displaymath}
Z(s) = [1 - A_0 - \int_0^1\,dx{\cal A}(x)] + A_0\frac{\sigma...
..._0^1\,dx{\cal A}(x)
\frac{\sigma_2}{(1-x)\sigma_1+x\sigma_2}.
\end{displaymath}](img144.gif) |
(47) |
Substituting this back into the original definition (41),
we find the symmetrical result
| 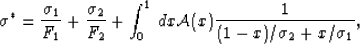 |
(48) |
where 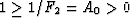 and
and
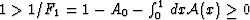 ,since
,since 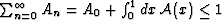 .The Fi's are known as ``formation factors''
(Archie, 1942; Avellandea and Torquato, 1991).
.The Fi's are known as ``formation factors''
(Archie, 1942; Avellandea and Torquato, 1991).
This equation is not yet in the same form as (40),
but it is nevertheless worthwhile to pause for a moment to consider
this form on its own merits. In particular,
the first two terms on the right hand side
are exactly what is expected when conductors are connected in parallel
inside a complex conducting medium. And the remaining integral looks
like some sort of weighted average of conductors connected in series.
The first physical analogy (conductors in parallel) is entirely
appropriate. The second one is no doubt an oversimplification of what is
happening in the medium, since the weights in the denominator
(i.e., x and 1-x) are not really volume fractions (even though they do
range from 0 to 1), and the density functional 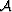 in the
numerator also contributes important numerical
weights depending on the local shapes and interconnectedness of the
microstructure of the conductors. This dependence on microstructure would
correspond approximately to the network connectivity in a resistor
network, but usually does not have a perfect analog for most 3D conducting
composites.
in the
numerator also contributes important numerical
weights depending on the local shapes and interconnectedness of the
microstructure of the conductors. This dependence on microstructure would
correspond approximately to the network connectivity in a resistor
network, but usually does not have a perfect analog for most 3D conducting
composites.
To complete the derivation of (40), we now need only
to make the further substitutions x = 1/(1+y) where y ranges from to
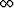 , and define
, and define 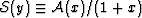 . Then, we arrive
finally at precisely (40), having found that S(1,0) = 1/F1
and S(0,1) = 1/F2. Furthermore, taking the limit
. Then, we arrive
finally at precisely (40), having found that S(1,0) = 1/F1
and S(0,1) = 1/F2. Furthermore, taking the limit
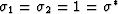 , we find the useful sumrule
, we find the useful sumrule
| 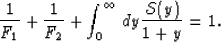 |
(49) |
Clearly, other choices of the integral transform in (48)
may also be useful. In particular, taking instead x = 1/(1-y) is
a good choice in preparation for analysis of the resonance density
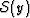 itself, as this transform places it most appropriately
on the negative real axis. But for present purposes either
(40) or (48)
is a satisfactory choice for study.
itself, as this transform places it most appropriately
on the negative real axis. But for present purposes either
(40) or (48)
is a satisfactory choice for study.





Next: Formation factor bounds
Up: CONDUCTIVITY: CANONICAL FUNCTIONS AND
Previous: Comparisons of conductivity bounds
Stanford Exploration Project
5/3/2005
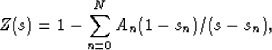
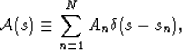
![]() in the
numerator also contributes important numerical
weights depending on the local shapes and interconnectedness of the
microstructure of the conductors. This dependence on microstructure would
correspond approximately to the network connectivity in a resistor
network, but usually does not have a perfect analog for most 3D conducting
composites.
in the
numerator also contributes important numerical
weights depending on the local shapes and interconnectedness of the
microstructure of the conductors. This dependence on microstructure would
correspond approximately to the network connectivity in a resistor
network, but usually does not have a perfect analog for most 3D conducting
composites.
![]() , and define
, and define ![]() . Then, we arrive
finally at precisely (40), having found that S(1,0) = 1/F1
and S(0,1) = 1/F2. Furthermore, taking the limit
. Then, we arrive
finally at precisely (40), having found that S(1,0) = 1/F1
and S(0,1) = 1/F2. Furthermore, taking the limit
![]() , we find the useful sumrule
, we find the useful sumrule
![]() itself, as this transform places it most appropriately
on the negative real axis. But for present purposes either
(40) or (48)
is a satisfactory choice for study.
itself, as this transform places it most appropriately
on the negative real axis. But for present purposes either
(40) or (48)
is a satisfactory choice for study.