Formation factor bounds

In a porous medium, when $\sigma_2 = \hbox{const}$ and $\sigma_1$ varies [as would be expected in a series of electrical conductivity experiments with different conducting fluids -- such as brines (Wildenschild et al., 2000) -- in the same pores], then general bounds can be derived from the form of (40). These bounds [see Berryman (2005a) for the full derivation] are given by  

$$\min(L_1,L_2) \le \sigma^*(\sigma_1,\sigma_2) \le \max(L_1,L_2),$$ (50)

where L₁ and L₂ are defined, respectively, by  

$$L_1(\sigma_1,\sigma_2) \equiv \sigma_2 + \frac{\sigma_1-\sigma_2}{F_1},$$ (51)

and  

$$L_2(\sigma_1,\sigma_2) \equiv \sigma_1 + \frac{\sigma_2-\sigma_1}{F_2}.$$ (52)

If one of the $\sigma_i$'s varies while the other remains constant, L₁ and L₂ are both straight lines, crossing when $\sigma_1 = \sigma_2$. We call (50) the formation factor bounds. One of them (always the lower bound for conductivities) often provides nontrivial improvements over the Hashin-Shtrikman and Beran bounds as we shall demonstrate by example.

The bounds obtained this way are in fact special cases of some earlier bounds by Prager (1969) and Bergman (1976), as discusssed recently by Milton (2002, pp.580-581). The approach as described by Milton is based on Padé approximation methods (Torquato, 1985a; Milton, 2002), although the original papers did not couch the analysis in these terms. Besides the much simpler derivation permitted by direct analysis of the Bergman-Milton analytic formulas (Berryman, 2005a). the main technical difference between the results here and those of Prager and Bergman is that we have implicitly assumed that two distinct (possibly idealized) formation factors have actually been carefully measured. To do so in practice requires either extremely high or extremely low conductivities of one or the other conducting component, or it requires a careful extrapolation process based on multiple measurements (Berryman, 2005b). These assumed direct measurements (or an extrapolation process) are perfectly reasonable when one or the other component is actually (or nearly) an insulator (electrical or thermal) [see Guéguen and Palciauskas (1994) for a discussion]. On the other hand, Prager's approach differs from this by providing bounds directly from any and all measurements on the same system as the constituents or choices of physical constants to be measured are allowed to vary. Bergman's method is very similar in this regard to Prager's. In both cases, these methods were applied to real constants just as we have done, but generalization to complex constants is also possible (Milton, 2002).

In our present notation, Prager's bounds can also be written in terms of the canonical function $\Sigma$. Assuming that two measurements have been made of the formation factors, we have four bounds from Prager's results. Two of these are the same as the Wiener (1912) bounds, i.e., the mean and harmonic mean based on volume fractions. The other two bounds are given by  

$$\sigma^*_{P1} = \Sigma(x_1\sigma_1) \quad\hbox{and}\quad \sigma^*_{P2} = \Sigma(x_2\sigma_2),$$ (53)

where  

$$x_1 = \frac{v_2}{2(v_1F_1 - 1)}\quad\hbox{and}\quad x_2 = \frac{v_1}{2(v_2F_2 - 1)}.$$ (54)

Using Hashin-Shtrikman bounds, it is not difficult to show that x₁ and x₂ are both nonnegative and bounded above by unity. Also, since $\sigma_{HS}^\pm = \Sigma(\sigma_\pm)$, one of Prager's bounds is always lower than the lower HS bound, and therefore not an improved bound, so not of interest to us. Furthermore, the other Prager bound is always lower than the upper HS bound. We show in the examples that for the case considered here this bound is in fact a useful lower bound on $\sigma^*$ that has the right asymptotic behavior -- i.e., approaching the formation factor bounds for large ratios of the constituent conductivities.

Similarly, two of the Bergman bounds can be written as  

$$\sigma^*_{B1} = \Sigma(x_1\sigma_1 + (1-x_1)\sigma_2) \quad\... ...}\quad \sigma^*_{B2} = \Sigma((1-x_2)\sigma_1 + x_2\sigma_2),$$ (55)

where x₁ and x₂ were defined previously in (54). There are two other Bergman bounds, but these reduce exactly to the HS bounds for the case under consideration here. It is also clear from the monotonicity of the canonical function $\Sigma$ and the facts $0 \le x_1,x_2 \le 1$ that the Bergman bounds given in (55) must always lie between or on the HS bounds. Furthermore, it is easy to see also that $\sigma^*_{P1}\le \sigma^*_{B1}$ and that $\sigma^*_{P2}\le \sigma^*_{B2}$, so Bergman's lower bound will always be superior to Prager's lower bound.

Asaad (1955) performed a series of thermal conductivity measurements on three different sandstones. He also measured the electrical formation factor of each sample. This data set is therefore most interesting to us for testing the theory. When the pores are filled with an electrically conducting fluid, current flows (in saturated sandstone) mostly through the pore fluid because sand grains are generally poor electrical conductors (Guéguen and Palciauskas, 1994). When the pores are filled instead with air, heat flows mostly through the sand grains because air is a poor thermal conductor. So the thermal conductivity properties of samples is quite different from those of electrical conductivity. But the microgeometry is still the same and, therefore, the structure of the equations for thermal conductivity is exactly the same as in (40). For Asaad's sandstone sample D, we find that F₂^D = 3.72 (from thermal conductivity measurements) and F₁^D = 33.0 (from electrical conductivity measurements). The porosity of this sample was $\phi^D = 0.126$, so $x_1 \simeq 0.138$ and $x_2 \simeq 0.028$. With these values known, we can make comparisons between and among the various theoretical results available to us. In particular note that since x₂ is quite small, $\sigma_{B2}^*$will clearly be very close to (nearly indistinguishable from) the Hashin-Shtrikman upper bound when $\sigma_1/\sigma_2 \gt 1$.

The uncorrelated Hashin-Shtrikman bounds (29) apply to this problem, as do the Beran bounds (31) and (32). To apply the Hashin-Shtrikman bounds we need only the volume fractions, but to apply the Beran bounds we also need some estimate of the microstructure parameters (the $\zeta_i$'s). Sandstones having a low porosity like 0.126 might have fairly round grains, but the pores themselves will surely not be well-approximated by spheres. So the common choice $\zeta_i = v_i$ is probably not adequate for this problem. A better choice is available however, since the values of $\zeta_i$ and $\eta_i$ have been computed numerically for the penetrable sphere model (Berryman, 1985b; Torquato, 1985b; 2002). This model microstructure is very much like that of a sandstone and, therefore, should prove adequate for our present comparisons. For porosity v₁ = 0.126, the penetrable sphere model has the value $\zeta_1 \simeq 0.472$. Since both formation factors are known for these experimental data, the formation factor (FF$\pm$) bounds can also be applied without difficulty. Figure 3 shows the results. (Note that the units of the conductivity have been normalized so all the curves cross at unity on this plot in order to make the Figure universal.)

We will limit this discussion to the region $\sigma_1/\sigma_2 \ge 1$.We find that the formation factor upper bound is well above the Hashin-Shtrikman upper bound, which is above the Beran bound as expected. All the bounds cross at $\sigma_1/\sigma_2 = 1$, as is necessary. The lower bounds have more complicated behavior. The Beran lower bound is always superior to the Hashin-Shtrikman lower bound, but they are both quite close together for all values of the ratio $\sigma_1/\sigma_2 \gt 1$. Both bounds are also superior to the lower formation factor bound for values of $\sigma_1/\sigma_2$ ratio close to unity. But, for higher values of contrast in the range $\sigma_1/\sigma_2 \gt 12$,these two bounds become inferior to the formation factor lower bound. This result is expected since it is for the asymptotic regimes (very high or very low ratios of the conductivities) that one of the FF bounds tends to become an exact estimate. Neither the Hashin-Shtrikman lower bounds nor the Beran lower bounds can compete in this regime because they must allow for the possibility that the more poorly conducting component plays host to the more strongly conducting component. Measured formation factor values provide new information that largely determines the status of this important long-range spatial correlation feature (due to the presence or absence of such a host/inclusion arrangement) throughout the microstructure.

Bergman lower bounds are best for moderate to high values of the contrast ratio, and they asymptote to the formation factor lower bounds (as do the Prager lower bounds) in the very high contrast regime. Note that Beran lower bounds can be superior to the Bergman lower bounds for small contrast ratios, since they use different measures of microstructure ($\zeta_i$ instead of F_i).

 

DNmixed
Figure 5 Conductivity comparisons including formation factor bounds.

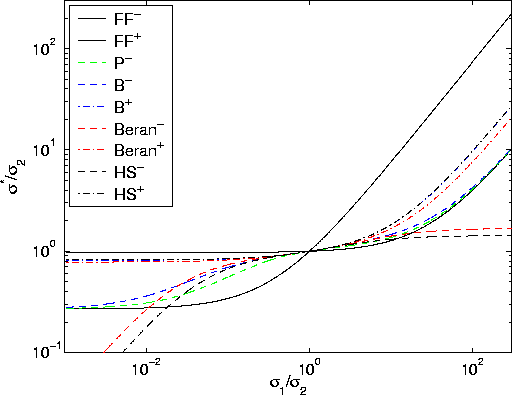Figure 5 shows comparisons of (a) the uncorrelated bounds of Hashin and Shtrikman (HS$^\pm$), (b) the microstructure-based bounds (assuming penetrable spheres) of Beran (Beran$^\pm$), (c) the Padé approximant bounds of Bergman (B$^\pm$) and Prager (P^-), and (d) the new formation factor (FF$^\pm$) bounds. Beran upper bounds are always the best ones shown here. Bergman lower bounds are best for moderate to high values of the contrast ratio, and they asymptote to the formation factor lower bounds (as do the Prager lower bounds) in the very high contrast regime. Beran lower bounds can be superior to the Bergman lower bounds for small contrast ratios. For the sake of universality, units of conductivity have been normalized so the curves all cross at unity.

So at high contrast ($\sigma_1/\sigma_2 \gg 1$), the Beran upper bound and the Bergman lower bound are the best (tightest) bounds for this sample sandstone D. For contrast ratios up to 300, we obtain bounds confining the conductivity to variations less than about a factor of 2, which will often be quite satisfactory for such difficult, but nevertheless fairly typical, estimation problems. The use of the formation factor lower bounds together with some of the earlier bounds like the Hashin-Shtrikman and Beran bounds therefore seems to be one satisfactory solution to some of the problems of high contrast conductivity estimation noted in the previous section. Otherwise, improvements can be made when desired using Prager, Bergman, and also Milton bounds (Milton, 1981b) [not discussed here]. Although the formation factor lower bounds are not the best known bounds, they are nevertheless very easy to use and give remarkably accurate estimates at very high contrasts.