Flattening Theory

The basic idea is similar to phase unwrapping Claerbout (1999), but instead of summing phase differences to get total phase, dips are summed to get total time shifts that are then used to flatten the data. To apply the shifts, a reference is held constant and all other traces are shifted vertically to match it.

The first step is to calculate dips everywhere in the 3-D seismic cube. Dip can be efficiently calculated using a plane-wave destructor as described in Claerbout (1992) or with an improved dip estimator that is described in Fomel (2002). We primarily use the latter. For each point in the data cube, two components of dip, p_x and p_y, are estimated in the x direction and y direction, respectively. These can be represented everywhere on the mesh as vectors ${\bf p}_x$ and ${\bf p}_y$.

Our goal is to find a time-shift (or depth-shift) field $\boldsymbol{\tau}(x,y,z)$ such that its gradient approximates the dip $\bf{p}\rm (x,y,\boldsymbol{\tau})$. Our objective function is:  

$$J(\boldsymbol{\tau}) = \int \int \left[ \left( {\bf p}_x(\bo... ...partial\boldsymbol{\tau}}{\partial y}\right)^2 \right] \,dx\,dy$$ (1)

The Euler-Lagrange equation is used in calculus of variations Farlow (1993) to find a function ($\boldsymbol{\tau}$) that will minimize a functional (J).

We apply the Euler-Lagrange equation to equation (1) to find:  

$$\frac{\partial^2 \boldsymbol{\tau}}{\partial x^2} + \frac{\p... ...tial({{\bf p}_x}^2+{{\bf p}_y}^2)}{\partial \boldsymbol{\tau}}.$$ (2)

In our method, we ignore the last term of equation (2) and iteratively solve:  

$$\frac{\partial^2 \boldsymbol{\tau}}{\partial x^2} + \frac{\p... ... {\bf p}_x}{\partial x}+ \frac{\partial {\bf p}_y}{\partial y}.$$ (3)

This equation can be rewritten using the gradient ($\boldsymbol\nabla=[ \frac{\partial }{\partial x} \; \; \frac{\partial }{\partial y}]'$) and the estimated dip (${\bf p} = [{\bf p}_x \; \; {\bf p}_y]'$)

$$\boldsymbol{\nabla}' \boldsymbol{\nabla} \boldsymbol{\tau}\quad = \quad \boldsymbol{\nabla}' \bf p .$$ (4)

Ultimately, the regression to be solved is:

$$\boldsymbol{\nabla} \boldsymbol{\tau}\quad = \quad \bf p .$$ (5)

This equation means that we need to find a time-shift field $\boldsymbol{\tau}(x,y,z)$ such that its gradient approximates the dip $\bf{p}\rm (x,y,\boldsymbol{\tau})$. Note that the estimated dip $\bf{p}\rm (x,y,\boldsymbol{\tau})$ field is a function of the unknown $\boldsymbol{\tau}(x,y,t)$ field, making this problem non-linear and, therefore, difficult to solve directly.

We solve this using a Gauss-Newton approach by iterating over equations (6)-(8)

		 iterate {    

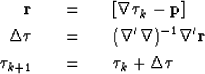$$\begin{eqnarray} \bf r \quad &=& \quad [\boldsymbol{\nabla} \boldsymbol{\tau}_k ... ...} \quad &=& \quad \boldsymbol{\tau}_{k} + \Delta \boldsymbol{\tau}\end{eqnarray}$$ (6) (7) (8)

		  }    

To dramatically improve efficiency, we solve equation (7) in the Fourier domain. We apply the divergence to the estimated dips and divide by the z-transform of the Laplacian in the Fourier domain with:  

$$\Delta \boldsymbol{\tau} \quad \approx \quad {\rm FFT_{\rm 2... ... r} \right]}\ \over { -Z_x^{-1} -Z_y^{-1} +4 -Z_x -Z_y} \right]$$ (9)

where $Z_x = e^{i w \Delta x} \$and$\ Z_y = e^{i w \Delta y}$.This amounts to calling both a forward and inverse FFT in each iteration. The ability to invert the 2D Laplacian in one step is the key to this method's exceptional performance.

Once we have converged the resulting time-shift field, $\boldsymbol{\tau}(x,y,t)$ contains all of the time-shifts required to map the original unflattened data to flattened data. This is implemented by applying the time-shifts relative to a reference trace. In other words, each trace is shifted to match the reference trace.

In general, we operate on a one-time slice at a time. After iterating until convergence, we then select the next time slice and proceed down through the cube. In this way, each time slice is solved independently.

The process of flattening tends to alter the spectrum of the data by stretching and compressing in time. Even worse, it can disrupt its continuity. To insure a monotonic and continuous result, it should be sufficient to first smooth the input dips in time (or depth). In some instances, it may be necessary to enforce smoothness during the integration of the dips. This can easily be accomplished by defining a 3D gradient operator with an adjustable smoothing parameter as:  

$${ \boldsymbol{\nabla}_\epsilon \boldsymbol{\tau} \quad = \qu... ...\ {\bf p}_y \\ 0 \end{array} \right] \quad = \quad {\bf p} }.$$ (10)

Our new operator $\boldsymbol{\nabla}_\epsilon$ has a scalar parameter $\epsilon$ used to control the amount of vertical smoothing. This requires integrating the entire 3D volume of dips at once rather than slice by slice. The 2D FFT's in equation (9) are replaced with 3D FFT's. Consequently, each iteration is slowed.

 

• Weighted solution for faults
• Computational cost