Weighted solution for faults

Local dips estimated at fault discontinuities can be inaccurate. We can, however, sum dips around the faults and ignore the spurious dips across the faults to get a flattened result.

We can add a weight to the residual to ignore fitting equations that are affected by the bad dips estimated at the faults. The regression to be solved is now:

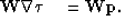$$\bf W \boldsymbol{\nabla} \boldsymbol{\tau}\quad = \bf W \bf p .$$ (11)

We iterate over the same equations as before, except equation (6) is now replaced with:  

$$\bf r \quad = \quad \bf W [\boldsymbol{\nabla} \boldsymbol{\tau}_k -\bf p]$$ (12)

Because we cannot apply a non-stationary weight in the Fourier domain, we use the same Fourier method as shown in equation (9). This means that the Fourier method is not approximating the inverse as well as before. The cost of this is more iterations, but method is still relatively efficient compared to other iterative methods. This approach is similar to Ghiglia and Romero (1994) for phase unwrapping.