Cost implications

Considering a data set with n_x receivers with n_t time samples, Table lists the number of operations required to construct shot-gathers by cross-correlating the traces of the transmission wavefield and migration of either the raw volume or the data volume produced by correlation. Under the conditions presented above, the n_ts time samples needed for the shot-gathers is the same as the number of frequencies required for direct migration. This will be orders of magnitude less than the n_t time samples collected during a passive seismic experiment in most cases. Finally, it is possible that not all receiver stations need be correlated when processing a large, high frequency experiment. $\nu$ will be a subsampling factor, less than 1, that controls the number of traces in, or aperture of, the correlated shot-gathers.

Migration costs scale according to the size of the input data set and the size of the image domain through which the data is extrapolated. X will represent a scalar multiplier due to the computer overhead costs of the migration strategy used. This will vary from a factor of  5 to n_x depending on the algorithm and accuracy required, but will be common to either direct migration or the migration of the correlated shot-gathers.

The size of the image space is assumed to be n_x samples areally by n_z samples in depth. No inverse Fourier transforms are required to prepare for migration, as the shot-gathers are needed to be functions of frequency for many migration algorithms. Also, I assume that the field passive seismic data fulfills the model of short source functions unevenly dispersed along the time axis of the duration of data collection.

 

 

$$\nu n_x^2 n_{ts}$$ Multiply

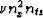$$(X n_z n_x) n_{ts}\nu n_x^2 \mbox{log}n_{x}$$ Gather Mig.

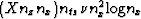$$(X n_z n_x) n_{ts} n_x \mbox{log}n_{x}$$ Raw Mig.

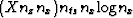With these costs in mind, the ratio of the sum of the first two rows to the last must be balanced to decide which choice requires the least amount of computation operations. When 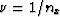$\nu = 1/n_x$, the costs of producing an image by either method is the same. The meaning of this situation is shot-gathers of one trace, i.e. a constant-offset (post-stack sized) migration. Thus, the passive seismic experiment acts similarly to a natural phase-encoding of active seismic shot-gathers that Romero et al. (2000) explains as a method to reduce the cost of shot-profile migration schemes. This can be thought of as performing a full prestack migration for the cost of a zero-offset migration.

Therefore, if it is appropriate to assume that potential subsurface seismic sources are reasonably short in duration, and that the length of the passive experiment is dictated by the requirement to collect a sufficient number of them to illuminate our image space, we can save substantial computation cost, orders of magnitude, by migrating the raw data directly. Even if one is concerned that such a severe decimation of the frequency axis might be detrimental, many safety multiples can be carried without affecting the speed-up of direct migration of the data.