Next: Cost implications
Up: Artman: Windowing passive data
Previous: 1D example
The seismic example was designed to mimic the passive seismic experiment and
reflects the injection of a few simple but very important assumptions
about the nature of the subsurface noise-field. These assumptions
immediately move us away from the truly random ambient noise
experiment. Strictly, I am assuming that the length of any particular
subsurface source is fairly short in duration i.e. less than a
few seconds) and randomly distributed throughout the recording time of the
experiment. Cross-talk between sources and their reflections about
the subsurface will be introduced under these assumptions if the
subsurface sources are not completely uncorrelated. Some degree of
correlation will arise if they are not separated in time by at least
the two-way traveltime to the deepest reflector and if the sources
have correlable waveforms.
Previously, I have manufactured synthetic passive data by convolving
transmission wavefields from individual sources with different, long,
random traces. The signal to noise ratio of the result can in this
case be shown to improve with the square root of the number of time
samples in the random source function and the square root of the
number of transmission wavefields, that is number of sources, used.
There are however important physical implications to modeling in this
manner. Specifically, it implies many sources exploding simultaneously
with infinite duration and perfect distribution of energy during this
entire period. A more reasonable experiment instead is one where the
sources have durations of less than a few seconds, and are randomly
distributed during the course of the recording interval.
The synthetic examples presented here are generated with random source
time functions no longer than 3 seconds and a random bulk time shift.
This facilitates the exploitation of this subsampling strategy to its
limit. Under these assumptions, increasing the signal-to-noise ratio
of the image will require recording more subsurface sources or
allowing the sources to ring for longer than 3 seconds. In either case, the
signal to noise ratio will increase with the square root of the
quantity considered.
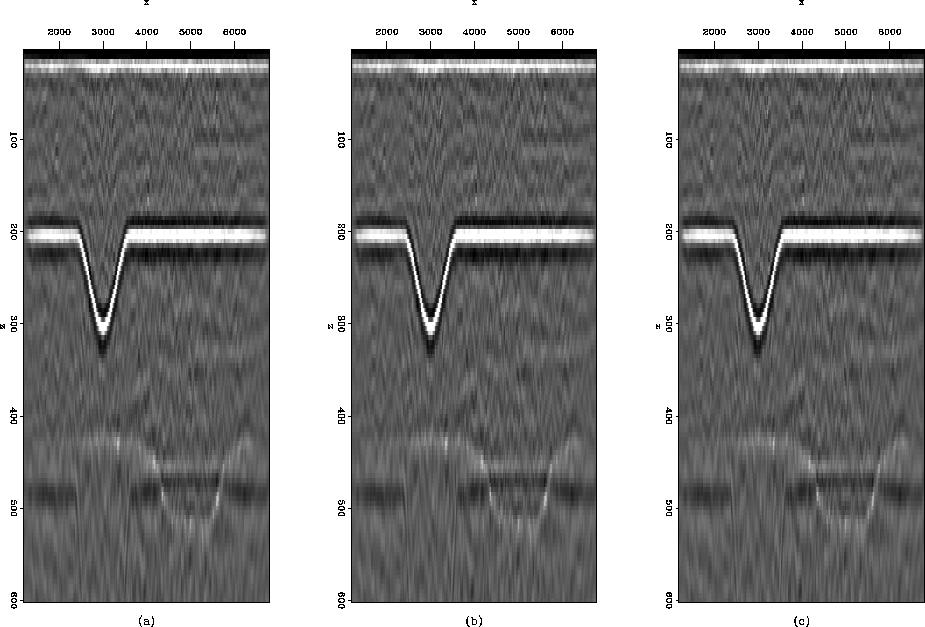
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) explores the use of Fourier subsampling on the
migration results of the synthetic passive data. Three data volumes
were created and imaged without first cross-correlating the traces Artman et al. (2004).
All three panels used 280
subsurface energy sources. The first panel was modeled with a total
experimental duration of 8 seconds. The second and third panels
assumed the recording time was 260 seconds. The first and second
panel directly migrated all the data from the entire recording
duration. They are identical to within machine precision. The third
panel subsampled the 260 second data set in the Fourier domain to a
level that will only support 4 seconds of an inverse Fourier
transform. This image is identical to the others.
explores the use of Fourier subsampling on the
migration results of the synthetic passive data. Three data volumes
were created and imaged without first cross-correlating the traces Artman et al. (2004).
All three panels used 280
subsurface energy sources. The first panel was modeled with a total
experimental duration of 8 seconds. The second and third panels
assumed the recording time was 260 seconds. The first and second
panel directly migrated all the data from the entire recording
duration. They are identical to within machine precision. The third
panel subsampled the 260 second data set in the Fourier domain to a
level that will only support 4 seconds of an inverse Fourier
transform. This image is identical to the others.
migsub
Figure 2 Identical imaging results from
direct migration of modeled
passive data from 280 subsurface sources (of random duration between
50 and 3000 ms) collected over 8 (panel (a)) and 260 (panels (b))
seconds and a version of the long data subsampled by a factor of 32
in the frequency domain (panel (c)).










Next: Cost implications
Up: Artman: Windowing passive data
Previous: 1D example
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) explores the use of Fourier subsampling on the
migration results of the synthetic passive data. Three data volumes
were created and imaged without first cross-correlating the traces Artman et al. (2004).
All three panels used 280
subsurface energy sources. The first panel was modeled with a total
experimental duration of 8 seconds. The second and third panels
assumed the recording time was 260 seconds. The first and second
panel directly migrated all the data from the entire recording
duration. They are identical to within machine precision. The third
panel subsampled the 260 second data set in the Fourier domain to a
level that will only support 4 seconds of an inverse Fourier
transform. This image is identical to the others.
explores the use of Fourier subsampling on the
migration results of the synthetic passive data. Three data volumes
were created and imaged without first cross-correlating the traces Artman et al. (2004).
All three panels used 280
subsurface energy sources. The first panel was modeled with a total
experimental duration of 8 seconds. The second and third panels
assumed the recording time was 260 seconds. The first and second
panel directly migrated all the data from the entire recording
duration. They are identical to within machine precision. The third
panel subsampled the 260 second data set in the Fourier domain to a
level that will only support 4 seconds of an inverse Fourier
transform. This image is identical to the others.