Next: Arbitrary scaling of velocity
Up: Anisotropic residual moveout for
Previous: Anisotropic residual moveout for
The derivative with respect to the perturbation component has the following particularly simple form:
|  |
(37) |
because the derivative of the slowness with respect to
a uniform scaling of the velocity has the following simple form:
| 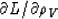 |
(38) |
that leads to the derivative
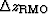 to be independent from the ``local'' shape of the anisotropic slowness function.
Intuitively, this simplification is related to the fact
that the ``shape'' of the wavefronts is not affected
by a uniform scaling of the velocity.
to be independent from the ``local'' shape of the anisotropic slowness function.
Intuitively, this simplification is related to the fact
that the ``shape'' of the wavefronts is not affected
by a uniform scaling of the velocity.
The residual moveout 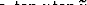 is defined as the difference
between the reflector movement at finite aperture angle
is defined as the difference
between the reflector movement at finite aperture angle 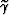 and the reflector movement at normal incidence.
From equation 38 the partial derivative
of
and the reflector movement at normal incidence.
From equation 38 the partial derivative
of 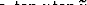 with respect to is equal to the
following expression:
with respect to is equal to the
following expression:
| 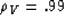 |
(39) |
When the medium is isotropic, and the
phase angles are equal to the group angles,
the RMO expression in equation 40
becomes the RMO expression introduced
by Biondi and Symes (2003).
The dependency of equation 40
from the group angles makes its use in
RMO analysis somewhat less convenient,
because it requires the transformation
of phase angles (measured directly from the image)
into group angles by applying equation 1.
The computational cost of evaluating equation 1
is negligible, but its use makes the computations
dependent on the local values of the background
anisotropic velocity function.
On the other hand, the following numerical examples show that
substantial errors are introduced when
the distinction between the group and phase angles
is neglected,
and the phase angle is used instead of the group
angle in equation 40.
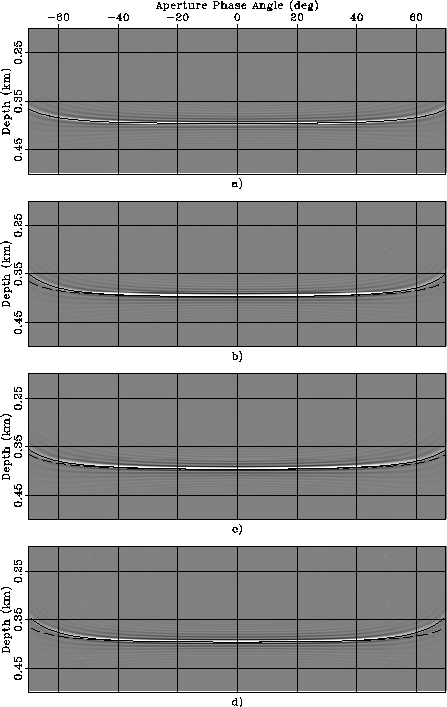
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows ADCIGs when an anisotropic velocity
was perturbed by
shows ADCIGs when an anisotropic velocity
was perturbed by 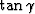 .The four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed by computing
.The four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed by computing
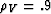 from
from 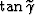 by applying equation 1,
whereas the dashed line was computed
by approximating
by applying equation 1,
whereas the dashed line was computed
by approximating 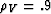 as equal to
as equal to 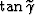 .The RMO curves computed using the
correct group angle perfectly match the
residual moveout of the images.
On the contrary,
when the phase angles are used instead of the group angles,
significant errors
are introduced even for such a small perturbation in the parameters
(
.The RMO curves computed using the
correct group angle perfectly match the
residual moveout of the images.
On the contrary,
when the phase angles are used instead of the group angles,
significant errors
are introduced even for such a small perturbation in the parameters
(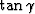 ).
It is interesting to notice that
the errors are larger for the rock types exhibiting
strong unelliptical anisotropy (Taylors Sand and GreenLight River Shale)
than for the strongly anisotropic
but quasi-elliptical rock (Mesa Clay Shale).
).
It is interesting to notice that
the errors are larger for the rock types exhibiting
strong unelliptical anisotropy (Taylors Sand and GreenLight River Shale)
than for the strongly anisotropic
but quasi-elliptical rock (Mesa Clay Shale).
The expression for the RMO function derived in
equation 40 is based on a linearization,
and thus
when the the perturbations in velocity parameters are large
it is not as accurate
as it is when the perturbations are small (e.g. 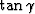 ).
Figure
).
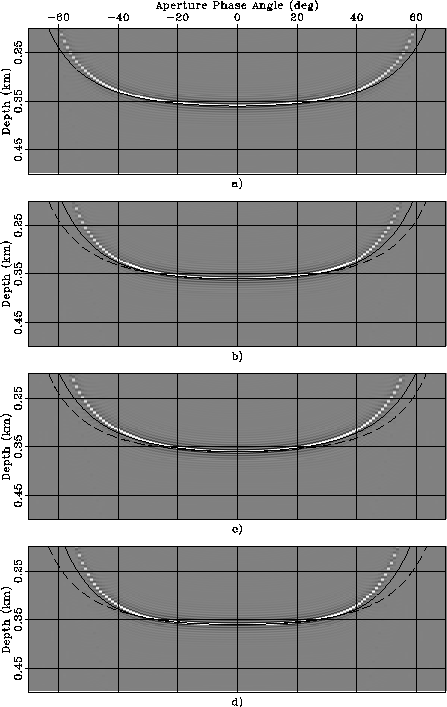
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this fact by
showing a similar experiment as the one shown in
Figure
illustrates this fact by
showing a similar experiment as the one shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
but with a perturbation 10 times larger;
that is, with .As in Figure
,
but with a perturbation 10 times larger;
that is, with .As in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale,
and the lines superimposed onto the images are the RMO functions
computed by using
the correct values for
,
the four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale,
and the lines superimposed onto the images are the RMO functions
computed by using
the correct values for 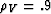 (solid lines),
and by using
(solid lines),
and by using 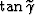 in place of
in place of 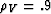 (dashed lines).
With large perturbations,
the predicted RMO functions differ from the actual RMO
functions at wide aperture angles
even when the correct values of the group angles are used
in equation 40.
However, even with such large perturbations
the predicted RMO functions are still useful approximations of the
actual RMO functions.
In particular, it can be observed that the
predicted RMO function correctly approximates the differences
in shape of the actual RMO function among the rock types.
These shape variations are related to the variations in shape of the wavefronts,
which are reflected in the predicted RMO function
through the variations in the mapping from phase angles to group angles.
(dashed lines).
With large perturbations,
the predicted RMO functions differ from the actual RMO
functions at wide aperture angles
even when the correct values of the group angles are used
in equation 40.
However, even with such large perturbations
the predicted RMO functions are still useful approximations of the
actual RMO functions.
In particular, it can be observed that the
predicted RMO function correctly approximates the differences
in shape of the actual RMO function among the rock types.
These shape variations are related to the variations in shape of the wavefronts,
which are reflected in the predicted RMO function
through the variations in the mapping from phase angles to group angles.
Quad_Aniso-rho.99_overn
Figure 7
ADCIGs obtained when a constant anisotropic velocity was perturbed by 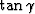 for four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed when
for four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed when 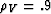 was derived from
was derived from 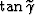 by applying equation 1,
whereas the dashed line was computed
by approximating
by applying equation 1,
whereas the dashed line was computed
by approximating 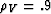 as equal to
as equal to 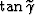 .
.





Quad_Aniso-rho.9_overn
Figure 8
ADCIGs obtained when a constant anisotropic velocity was perturbed by for four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed when 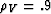 was derived from
was derived from 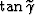 by applying equation 1,
whereas the dashed line was computed
by approximating
by applying equation 1,
whereas the dashed line was computed
by approximating 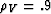 as equal to
as equal to 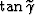 .
.










Next: Arbitrary scaling of velocity
Up: Anisotropic residual moveout for
Previous: Anisotropic residual moveout for
Stanford Exploration Project
5/3/2005


![]() is defined as the difference
between the reflector movement at finite aperture angle
is defined as the difference
between the reflector movement at finite aperture angle ![]() and the reflector movement at normal incidence.
From equation 38 the partial derivative
of
and the reflector movement at normal incidence.
From equation 38 the partial derivative
of ![]() with respect to is equal to the
following expression:
with respect to is equal to the
following expression:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows ADCIGs when an anisotropic velocity
was perturbed by
shows ADCIGs when an anisotropic velocity
was perturbed by ![]() .The four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed by computing
.The four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale.
Superimposed onto the images are the RMO functions
computed using equation 40.
The solid line was computed by computing
![]() from
from ![]() by applying equation 1,
whereas the dashed line was computed
by approximating
by applying equation 1,
whereas the dashed line was computed
by approximating ![]() as equal to
as equal to ![]() .The RMO curves computed using the
correct group angle perfectly match the
residual moveout of the images.
On the contrary,
when the phase angles are used instead of the group angles,
significant errors
are introduced even for such a small perturbation in the parameters
(
.The RMO curves computed using the
correct group angle perfectly match the
residual moveout of the images.
On the contrary,
when the phase angles are used instead of the group angles,
significant errors
are introduced even for such a small perturbation in the parameters
(![]() ).
It is interesting to notice that
the errors are larger for the rock types exhibiting
strong unelliptical anisotropy (Taylors Sand and GreenLight River Shale)
than for the strongly anisotropic
but quasi-elliptical rock (Mesa Clay Shale).
).
It is interesting to notice that
the errors are larger for the rock types exhibiting
strong unelliptical anisotropy (Taylors Sand and GreenLight River Shale)
than for the strongly anisotropic
but quasi-elliptical rock (Mesa Clay Shale).
![]() ).
Figure
).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this fact by
showing a similar experiment as the one shown in
Figure
illustrates this fact by
showing a similar experiment as the one shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
but with a perturbation 10 times larger;
that is, with .As in Figure
,
but with a perturbation 10 times larger;
that is, with .As in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale,
and the lines superimposed onto the images are the RMO functions
computed by using
the correct values for
,
the four panels correspond to four rock types:
a) Isotropic, b) Taylor Sand, c) Mesa Clay Shale,
and
d) GreenLight River Shale,
and the lines superimposed onto the images are the RMO functions
computed by using
the correct values for ![]() (solid lines),
and by using
(solid lines),
and by using ![]() in place of
in place of ![]() (dashed lines).
With large perturbations,
the predicted RMO functions differ from the actual RMO
functions at wide aperture angles
even when the correct values of the group angles are used
in equation 40.
However, even with such large perturbations
the predicted RMO functions are still useful approximations of the
actual RMO functions.
In particular, it can be observed that the
predicted RMO function correctly approximates the differences
in shape of the actual RMO function among the rock types.
These shape variations are related to the variations in shape of the wavefronts,
which are reflected in the predicted RMO function
through the variations in the mapping from phase angles to group angles.
(dashed lines).
With large perturbations,
the predicted RMO functions differ from the actual RMO
functions at wide aperture angles
even when the correct values of the group angles are used
in equation 40.
However, even with such large perturbations
the predicted RMO functions are still useful approximations of the
actual RMO functions.
In particular, it can be observed that the
predicted RMO function correctly approximates the differences
in shape of the actual RMO function among the rock types.
These shape variations are related to the variations in shape of the wavefronts,
which are reflected in the predicted RMO function
through the variations in the mapping from phase angles to group angles.