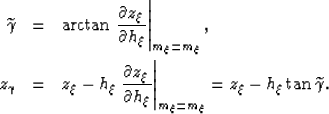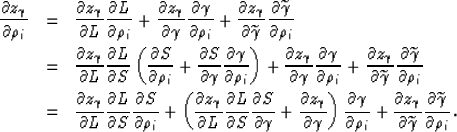Next: Uniform scaling of velocity
Up: Biondi: Anistropic ADCIGs
Previous: Numerical examples of aperture
The kinematic formulation of the generalized impulse response
presented in the previous section
enables a simple analysis of the residual moveout (RMO)
in ADCIGs caused by errors in anisotropic velocity parameters.
For the sake of simplicity, at the present,
I limit my analysis to reflections from flat interfaces.
However, a generalization of the flat-events analysis to
dipping events should be conceptually
straightforward, though not necessarily simple from the analytical
point of view.
A VTI velocity function, either group or phase, is described by the following
vector of three velocities 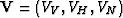 ,as for example used in equations 5,
or by the corresponding vector of three slownesses
,as for example used in equations 5,
or by the corresponding vector of three slownesses 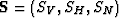 used in equation 6.
I define the perturbations as one multiplicative
factors for each of the velocities and one multiplicative factor
for all velocities;
that is, the perturbed velocity
used in equation 6.
I define the perturbations as one multiplicative
factors for each of the velocities and one multiplicative factor
for all velocities;
that is, the perturbed velocity 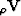 is defined as:
is defined as:
|  |
(30) |
The velocity-parameter perturbations is thus defined
by the following four-components vector
 =
=
 .
.
For flat reflectors,
the transformation to angle domain
maps an image point at coordinates 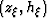 into an image point with coordinates
into an image point with coordinates 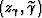 according to the following mapping:
according to the following mapping:
| 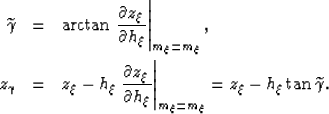 |
(31) |
| (32) |
The partial derivative of the angle-domain depth 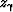 with respect to the i-th component in the perturbation vector
can be expressed as follows:
with respect to the i-th component in the perturbation vector
can be expressed as follows:
| 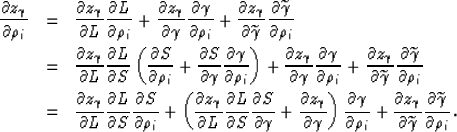 |
|
| |
| (33) |
In Appendix B I demonstrate that the
terms multiplying the partial derivatives
with respect to the angles are zero,
and equation 34 simplifies into:
| 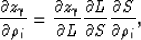 |
(34) |
where
| 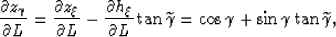 |
(35) |
and
|  |
(36) |
![]() ,as for example used in equations 5,
or by the corresponding vector of three slownesses
,as for example used in equations 5,
or by the corresponding vector of three slownesses ![]() used in equation 6.
I define the perturbations as one multiplicative
factors for each of the velocities and one multiplicative factor
for all velocities;
that is, the perturbed velocity
used in equation 6.
I define the perturbations as one multiplicative
factors for each of the velocities and one multiplicative factor
for all velocities;
that is, the perturbed velocity ![]() is defined as:
is defined as:
![]() into an image point with coordinates
into an image point with coordinates ![]() according to the following mapping:
according to the following mapping: