




Next: PEFs in the data
Up: Curry: Interpolating with data-space
Previous: INTRODUCTION
The Madagascar regularization problem has been approached using the following fitting goals Lomask (2002):
| ![\begin{eqnarray}
\ {\bf W} \frac{d}{dt}[{\bf L}{\bf m} -{\bf d}] &\approx& {\bf 0} \nonumber \\ \ \epsilon {\bf A m} &\approx& {\bf 0} .
\end{eqnarray}](img1.gif) |
|
| (1) |
In these fitting goals: W corresponds to a weight for ends of tracks and spikes in the data, 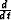 is a derivative along each track used to
eliminate low frequency variations along each track,
L is a linear interpolation operator that moves from values on a regular grid to the data points,
m is the desired gridded model, d are the data points along the tracks, A is a regularization operator, and
is a derivative along each track used to
eliminate low frequency variations along each track,
L is a linear interpolation operator that moves from values on a regular grid to the data points,
m is the desired gridded model, d are the data points along the tracks, A is a regularization operator, and  is a trade-off
parameter between the two fitting goals.
is a trade-off
parameter between the two fitting goals.
The regularization operator (A) typically is a Laplacian, a prediction-error filter (PEF), or a non-stationary PEF Crawley (2000). When using a PEF,
it first must be estimated on some training data, using a least-squares fitting goal,
| 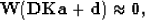 |
(2) |
in which W is a weight to exclude equations with missing data, D is convolution with the data, K constrains the
first filter coefficient to 1, a is the unknown filter, and d is a copy of the data.
data
Figure 1 (a) sparse tracks. (b)
dense tracks.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





In order to set a benchmark for how effective any interpolation of the
sparse tracks is,
a PEF is estimated using fitting goal (2) on the output of fitting goals (1) when
using the dense tracks of the Madagascar dataset and a Laplacian
regularization operator. The PEF is then used to interpolate the sparse
tracks in the same area, using the same fitting goals (1),
this time with the regularization being convolution with a
PEF. This result provides an upper bound to what an ideal
interpolation of the data would be if we already knew the answer. Any
new result should be much better than the Laplacian regularization
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
b.
best
Figure 2 (a) dense data regularized with
a Laplacian. (b) sparse data regularized with a
Laplacian. (c) sparse data regularized with a PEF trained on the
top.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: PEFs in the data
Up: Curry: Interpolating with data-space
Previous: INTRODUCTION
Stanford Exploration Project
5/3/2005
![\begin{eqnarray}
\ {\bf W} \frac{d}{dt}[{\bf L}{\bf m} -{\bf d}] &\approx& {\bf 0} \nonumber \\ \ \epsilon {\bf A m} &\approx& {\bf 0} .
\end{eqnarray}](img1.gif)
![\begin{eqnarray}
\ {\bf W} \frac{d}{dt}[{\bf L}{\bf m} -{\bf d}] &\approx& {\bf 0} \nonumber \\ \ \epsilon {\bf A m} &\approx& {\bf 0} .
\end{eqnarray}](img1.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
b.

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)