 |
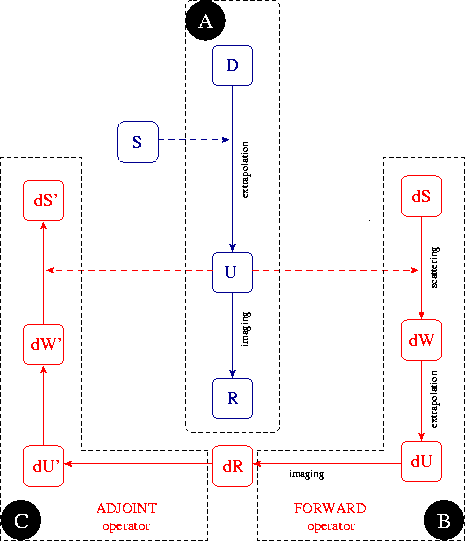
Figure 1 WEMVA flowchart. Box A: background wavefield. Box B: forward WEMVA operator. Box C: adjoint WEMVA operator.
 |
The computation of the velocity updates from the results of migrating the data with the current (background) velocity model comprises three main components that are summarized by the flow-chart in wemva_chart. The three components are labeled as A, B and C on the chart. Box A corresponds to the computation of the background wavefield, based on the surface data and background slowness. Boxes B and C correspond respectively to the forward and adjoint WEMVA operator.
The data recorded at the surface (D) are downward continued using wavefield extrapolation to all depth levels using the background slowness (S), to generate a background wavefield (U). The known background slowness (S) can incorporate lateral variations. Extrapolation can be done with kernels corresponding to such methods as Fourier finite-difference (81), or generalized screen propagator (85). From the extrapolated wavefield, we can construct the background image (R) by applying a standard imaging condition, for example a simple summation over frequencies.
The background wavefield (U) is an important component of the WEMVA operator. This wavefield plays a role analogous to the one played in traveltime tomography by the rayfield obtained by ray tracing in the background model. The wavefield is the carrier of information and defines the multivalued wavepaths along which we spread the velocity errors measured from the migrated images obtained using the background slowness function. The wavefield is band limited, unlike a rayfield which describes propagation of waves with an infinite frequency band. Therefore, the background wavefield provides a more accurate description of wave propagation through complicated media than a corresponding rayfield. Typical examples are salt bodies characterized by large velocity contrasts where ray tracing is both unstable and inaccurate.
When evaluating the forward operator (Box B), the background wavefield (U) interacts with a slowness perturbation (dS) and generates a scattered wavefield (dW) at every depth level. In this method, scattering is based on the first-order Born approximation, which assumes perturbations to be small both in size and magnitude. This approximation is appropriate, because scattering occurs independently at every depth level. The contribution to the scattered wavefield, is added at each depth level, and the total scattered wavefield (dU) is extrapolated to depth, using the same numerical propagator as the one used to extrapolate the background wavefield from the surface data. Therefore, the wavefield perturbation at any depth level contains the accumulated effects of scattering and extrapolation from all the levels above it. Finally, I apply an imaging condition to the wavefield perturbation (dU) and obtain an image perturbation (dR) corresponding to the slowness perturbation (dS) and the background wavefield (U).
In migration velocity analysis, we are interested in the inverse process, where we take an image perturbation (dR) and construct a slowness perturbation (dS). We obtain image perturbations via image enhancement operators (residual moveout, residual migration etc.) applied to the background image (R). Since the scattering operator is based on the Born approximation, we need to take special precautions to avoid cycle-skipping of phase function. I overcome the Born approximation limitations by using linearized image perturbations discussed in a following section.
To invert the linearized image perturbation into slowness updates by an iterative algorithm, such as conjugate directions, we need to evaluate the adjoint WEMVA operator (Box C) as well as the forward operator. From the image perturbation (dR), we can construct an adjoint wavefield perturbation (dU) by applying the adjoint imaging operator. This wavefield is then upward continued to all levels and an adjoint scattered wavefield (dW') is accumulated. Finally, using the background wavefield (U), we can generate the adjoint slowness perturbation (dS').
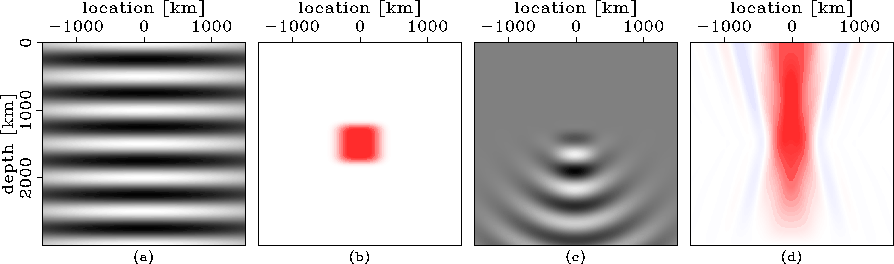 |
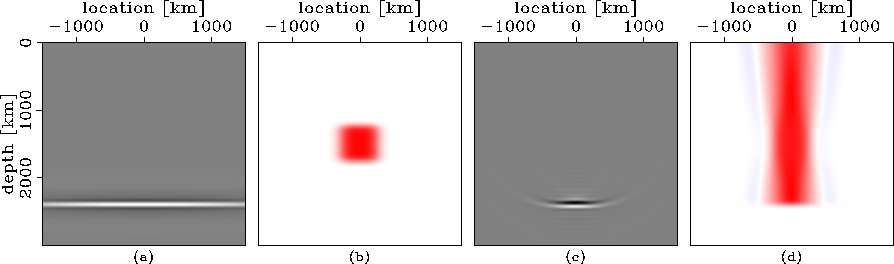
SCATbas1.scat and SCATbasN.scat illustrate the flow-chart shown in wemva_chart by showing its application to two simple examples. In the first example (SCATbas1.scat), I use a monochromatic wavefield, whereas in the second one (SCATbasN.scat), I use a wideband wavefield. For both examples the data are recorded above a planar horizontal reflector.
SCATbas1.scata shows a snapshot (taken at time zero) of the monochromatic background wavefield obtained by downward continuation of an incident plane wave in a constant medium. SCATbas1.scatb shows a slowness perturbation, that under the influence of the incident wavefield (a), generates a wavefield perturbation (c). The snapshots at zero time shown in panels (a) and (c) can also be regarded as images. Finally, I backpropagate the image perturbation (c) and obtain the adjoint slowness perturbation (d).
SCATbasN.scat shows the analogous panels shown SCATbas1.scat, but for wide-band data. SCATbasN.scata shows the image obtained by wavefield extrapolation of a wide-band plane wave in the background medium. From the same slowness perturbation (b) as in the preceding example, I obtain an image perturbation (c), from which I generate an adjoint slowness perturbation (d) using the background wavefield used to compute the background image.
 |