




Next: Examples
Up: Theory
Previous: Space-domain solution
Mixed-domain solutions to the one-way wave equation usually
consist of terms computed in the Fourier domain for a
reference of the extrapolation medium, followed by a
finite-differences correction applied in the space-domain.
For equation (9), a generic mixed-domain solution has the
form:
| 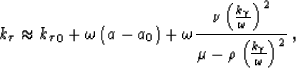 |
(13) |
where a0 and b0 are reference values for the
medium characterized by the parameters a and b,
and the coefficients 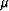 ,
,  and
and 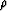 take
different forms according to the type of approximation.
As for usual Cartesian coordinates,
take
different forms according to the type of approximation.
As for usual Cartesian coordinates,
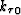 is applied in the Fourier domain, and
the other two terms are applied in the space domain.
If we limit the space-domain correction to the
thin lens term,
is applied in the Fourier domain, and
the other two terms are applied in the space domain.
If we limit the space-domain correction to the
thin lens term, 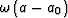 , we obtain the
equivalent of split-step Fourier (SSF) method
Stoffa et al. (1990) in Riemannian coordinates.
, we obtain the
equivalent of split-step Fourier (SSF) method
Stoffa et al. (1990) in Riemannian coordinates.
Appendix A details the derivations for two types of expansions:
pseudo-screen Huang et al. (1999), and
Fourier finite-differences Biondi (2002); Ristow and Ruhl (1994).





Next: Examples
Up: Theory
Previous: Space-domain solution
Stanford Exploration Project
10/23/2004
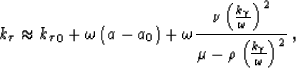
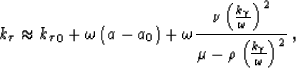
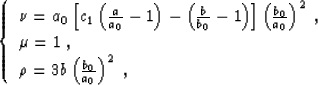
![\begin{displaymath}
k_\tau\approx {k_\tau}_0+ \omega
\left [1+ \frac{ \frac{ c_1...
...k_\gamma}{ \omega}\right )^2}
\right ]\left (s-s_0 \right )\;,\end{displaymath}](img33.gif)
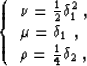
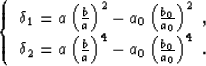
![\begin{displaymath}
k_\tau\approx {k_\tau}_0+ \omega
\left [1+ \frac{ \frac{c_1}...
...k_\gamma}{ \omega}\right )^2}
\right ]\left (s-s_0 \right )\;,\end{displaymath}](img36.gif)