




Next: Theory
Up: Sava: Riemannian wavefield extrapolation
Previous: Introduction
Riemannian wavefield extrapolation Sava and Fomel (2003)
generalizes solutions to the Helmholtz equation
| 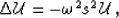 |
(1) |
to coordinate systems that are different from simple Cartesian,
where extrapolation is performed strictly in the downward direction.
In equation (1), s is slowness, 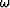 is temporal frequency,
and
is temporal frequency,
and 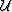 is a monochromatic wave.
is a monochromatic wave.
The acoustic wave-equation in Riemannian coordinates
can be written as:
| 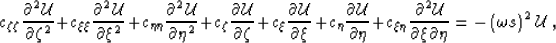 |
(2) |
where coefficients cij
are functions of the coordinate system and can
be computed numerically for any given coordinate system
Sava and Fomel (2003).
We can simplify the Riemannian wavefield extrapolation method
by dropping the first-order terms in equation (2).
According to the theory of characteristics for
second-order hyperbolic equations Courant and Hilbert (1989),
these terms affect only the amplitude of the propagating waves.
To preserve the kinematics, it is sufficient to keep only the
second order terms of equation (2):
| 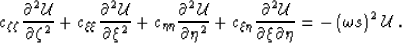 |
(3) |
From equation (3) we can derive the following
dispersion relation:
| 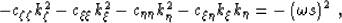 |
(4) |
where 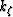 ,
, 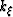 and
and 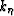 are wavenumbers associated
with the Riemannian coordinates
are wavenumbers associated
with the Riemannian coordinates 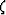 ,
, 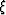 and
and  .
.
For one-way wavefield extrapolation, we need to solve
the quadratic equation (4)
for the wavenumber of the extrapolation direction 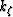 ,and select the solution with the appropriate sign to
extrapolate waves in the desired direction:
,and select the solution with the appropriate sign to
extrapolate waves in the desired direction:
| 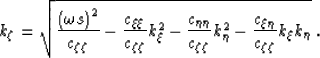 |
(5) |
The 2D equivalent of equation (5) takes the form:
| 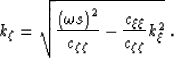 |
(6) |
In ray coordinates,
defined by 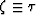 and
and 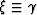 ,
we can re-write equation (6) as
,
we can re-write equation (6) as
| 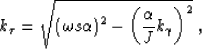 |
(7) |
where  is velocity and J is geometrical spreading.
We can simplify the computations by the notation
is velocity and J is geometrical spreading.
We can simplify the computations by the notation
| 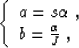 |
(8) |
therefore, equation (7) takes the form
| 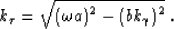 |
(9) |





Next: Theory
Up: Sava: Riemannian wavefield extrapolation
Previous: Introduction
Stanford Exploration Project
10/23/2004
![]() ,and select the solution with the appropriate sign to
extrapolate waves in the desired direction:
,and select the solution with the appropriate sign to
extrapolate waves in the desired direction:
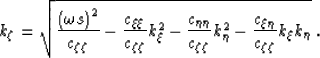
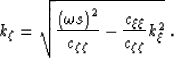
![]() and
and ![]() ,
we can re-write equation (6) as
,
we can re-write equation (6) as