




Next: MODEL OF HETEROGENEOUS RESERVOIRS
Up: Berryman: Bounds on geomechanical
Previous: ELASTICITY OF LAYERED MATERIALS
As a first result, consider a laminated grain composed of isotropic
constituents, all having the same bulk modulus K in each layer, but
differing shear moduli. Then, if we define the function
[compare (1)]
| ![\begin{displaymath}
g(\zeta) = \left[\sum_{n=1}^{N} \frac{f_n}{\mu_n+\zeta}\right]^{-1}
- \zeta,
\end{displaymath}](img22.gif) |
(6) |
we find from (3)
that 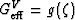 with
with 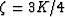 .This function
.This function 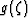 has the interesting and useful properties that
has the interesting and useful properties that
| 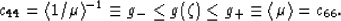 |
(7) |
Furthermore, 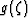 is a monotonic function, achieving its lower
bound when
is a monotonic function, achieving its lower
bound when 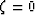 and approaching its upper bound as
and approaching its upper bound as 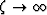 .This formula shows in an elementary way how
.This formula shows in an elementary way how
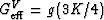 -- and therefore
-- and therefore 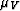 --
depends on the constant bulk modulus of the system, and
also that this component of the Voigt bound on the
overall shear modulus increases with increasing magnitude of the
bulk modulus. The overall Voigt bound/estimate (5)
for shear therefore has very similar character, but the magnitude
of the effect is reduced by a factor of 5, since this is only one of
the five distinct contributors to the overall shear behavior of the
system. So the largest change in the Voigt shear modulus that variations
in bulk modulus can ever induce are expected to be on the order
of 20% (or less) of the difference c66-c44.
--
depends on the constant bulk modulus of the system, and
also that this component of the Voigt bound on the
overall shear modulus increases with increasing magnitude of the
bulk modulus. The overall Voigt bound/estimate (5)
for shear therefore has very similar character, but the magnitude
of the effect is reduced by a factor of 5, since this is only one of
the five distinct contributors to the overall shear behavior of the
system. So the largest change in the Voigt shear modulus that variations
in bulk modulus can ever induce are expected to be on the order
of 20% (or less) of the difference c66-c44.
Similarly, the Reuss average for shear is
| ![\begin{displaymath}
\mu_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^R} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img31.gif) |
(8) |
which is also a rigorous lower bound on the overall shear modulus of
the polycrystal (Hill, 1952). For each hexagonal grain, the product formulas
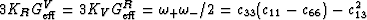 are valid. The symbols
are valid. The symbols 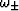 stand for the quasi-compressional and quasi-uniaxial shear eigenvalues
for all the grains (Berryman, 2004). The product formulas show immediately that
stand for the quasi-compressional and quasi-uniaxial shear eigenvalues
for all the grains (Berryman, 2004). The product formulas show immediately that
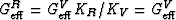 , since
KR = KV = K. Thus, for this relatively simple system,
pure compression or tension (e11 = e22 = e33) is an eigenvector
corresponding to stiffness eigenvalue 3K.
Uniaxial shear strain (e33 = -2e11 = -2e22)
is also an eigenvector and
, since
KR = KV = K. Thus, for this relatively simple system,
pure compression or tension (e11 = e22 = e33) is an eigenvector
corresponding to stiffness eigenvalue 3K.
Uniaxial shear strain (e33 = -2e11 = -2e22)
is also an eigenvector and 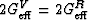 is the
corresponding eigenvalue.
is the
corresponding eigenvalue.





Next: MODEL OF HETEROGENEOUS RESERVOIRS
Up: Berryman: Bounds on geomechanical
Previous: ELASTICITY OF LAYERED MATERIALS
Stanford Exploration Project
10/23/2004
![\begin{displaymath}
g(\zeta) = \left[\sum_{n=1}^{N} \frac{f_n}{\mu_n+\zeta}\right]^{-1}
- \zeta,
\end{displaymath}](img22.gif)
![\begin{displaymath}
g(\zeta) = \left[\sum_{n=1}^{N} \frac{f_n}{\mu_n+\zeta}\right]^{-1}
- \zeta,
\end{displaymath}](img22.gif)
![\begin{displaymath}
\mu_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^R} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img31.gif)