
We assume that a typical building block of the random system is a small grain of laminate material whose elastic response for such a transversely isotropic (hexagonal) system can be described by:
 |
(2) |
Although some of the results presented here are more general, we will
assume for definiteness that this stiffness matrix in
(2) arises from
the lamination of N isotropic constituents having bulk and shear
moduli Kn, ![]() , in the N > 1 layers present in each
building block. It is important that the thicknesses dn always be
in the same proportion in each of these laminated blocks, so that
, in the N > 1 layers present in each
building block. It is important that the thicknesses dn always be
in the same proportion in each of these laminated blocks, so that
![]() . But it is
not important what order the layers were added to the blocks, as
Backus's formulas (Backus, 1962)
for the constants show. For the overall
behavior for the quasistatic (long wavelength) behavior of the system
we are studying, Backus's results [also see Postma (1955) and Milton
(2002)]
state that
. But it is
not important what order the layers were added to the blocks, as
Backus's formulas (Backus, 1962)
for the constants show. For the overall
behavior for the quasistatic (long wavelength) behavior of the system
we are studying, Backus's results [also see Postma (1955) and Milton
(2002)]
state that
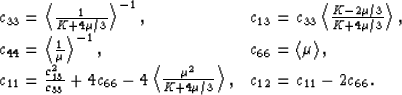 |
(3) |
The bulk modulus for each such building block (or crystalline grain if
you like) is that given by the compressional Reuss average KR
of the corresponding compliance matrix sij [the inverse of the
usual stiffness matrix cij, whose nonzero components are
shown in (2)]. The well-known result is
![]() , where
, where
![]() .This quantity can be expressed in terms of the stiffness elements as
.This quantity can be expressed in terms of the stiffness elements as
| |
(4) |
Even though ![]() is the same for every grain, since the
grains themselves are not isotropic, the overall bulk modulus
K* of the random polycrystal is not necessarily the same as
is the same for every grain, since the
grains themselves are not isotropic, the overall bulk modulus
K* of the random polycrystal is not necessarily the same as
![]() for the individual grains (Hill, 1952). Hashin-Shtrikman bounds on K* for random polycrystals whose
grains have hexagonal symmetry
(Peselnick and Meister, 1965; Watt and Peselnick, 1980)
show in fact that the value KR lies outside the bounds
in many situations. We will say more about this in the fourth section.
for the individual grains (Hill, 1952). Hashin-Shtrikman bounds on K* for random polycrystals whose
grains have hexagonal symmetry
(Peselnick and Meister, 1965; Watt and Peselnick, 1980)
show in fact that the value KR lies outside the bounds
in many situations. We will say more about this in the fourth section.
In general an upper bound on the overall shear modulus of an isotropic polycrystal (Hill, 1952) is given by the Voigt average over shear of the stiffness matrix, which may be written as
| |
(5) |