MODEL OF HETEROGENEOUS RESERVOIRS

Returning to the general problem for arbitrary K_n, suppose we construct a random polycrystal by packing small bits of this laminate material into a large container in a way so that the axis of symmetry appears randomly over all possible orientations and also such that no empty volume (porosity) is left in the resulting composite. If the ratio of grain size to overall composite is small enough so the usual implicit assumption of scale separation applies to the composite -- but not so small that we are violating the continuum hypothesis -- then we have an example of the type of material we want to study.

For each individual grain in this polycrystal, Eqs. (3) are valid locally (i.e., for locally defined coordinates), and the grain bulk modulus K_R is given by (4) for all the grains. The factors 3K_R and $2G_{\rm eff}^V$ are not necessarily eigenvalues of elastic stiffness for individual grains. The Voigt average for shear is again given by (5), which is an upper bound on the isotropic shear modulus of the random polycrystal (Hill, 1952).

 

K4bounds Figure 1 Various bulk modulus bounds: The outer most bounds (blue dot-dash lines) are the standard Hashin-Shtrikman bounds (HS) based only on information about the layer constituents and their volume fractions. The black solid lines are the Voigt and Reuss bounds (XV,XR) obtained from appropriate averages of laminate constants in (3). The inner most bounds (also blue dot-dash lines) are the Peselnick-Meister bounds (PM) for hexagonal polycrystals. For contrast, the Dederich-Zeller bounds (DZ) (see Appendix B) are also shown (dashed red lines).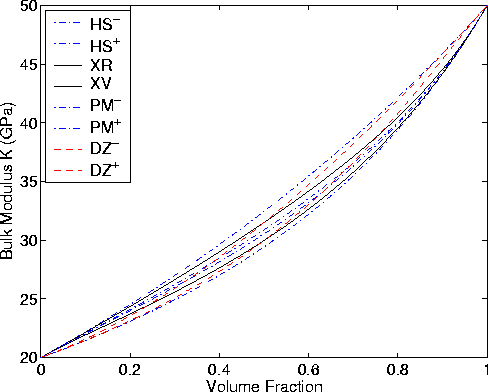

 

mu4bounds Figure 2 Same as Figure 1 for the various shear modulus bounds.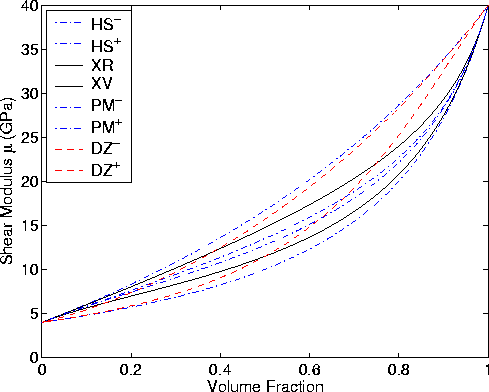

The advantage of studying polycrystals of laminates is that we have available an array of theoretical results from which to choose. For example, since each grain is composed of isotropic constitutents, standard Voigt and Reuss bounds (Hill, 1952), as well as the more restrictive Hashin-Shtrikman bounds (Hashin and Shtrikman, 1962; 1963) on composites made up of isotropic constituents are all available. Then, we can instead, or in addition, consider Voigt and Reuss bounds on the laminated grain materials. Formulas for these bounds have already been given here in Eqs. (4), (5), and (8), respectively for K_R, $\mu_V$, and $\mu_R$.The remaining formula is well-known to be  

$$K_V = \left[2(c_{11}+c_{12}) +4c_{13}+c_{33}\right]/9.$$ (9)

Then, it is useful to distinguish between ``correlated'' and ``uncorrelated'' bounds. For example, the most familiar bounds -- after the uncorrelated Voigt and Reuss bounds (i.e., the volume averaged mean and harmonic mean respectively of the consitutents' constants) -- are the uncorrelated Hashin-Shtrikman bounds:  

$$K_{HS}^{\pm}= \left[\sum_{n=1}^{N} \frac{f_n}{K_n+4\mu_\pm/3}\right]^{-1} - 4\mu_\pm/3$$ (10)

and  

$$\mu_{HS}^{\pm}= \left[\sum_{n=1}^{N} \frac{f_n}{\mu_n+\zeta_\pm}\right]^{-1} - \zeta_\pm,$$ (11)

where  

$$\zeta_\pm = \frac{\mu_\pm}{6} \left(\frac{9K_\pm+8\mu_\pm}{K_\pm+2\mu_\pm}\right),$$ (12)

with K₊ and K_- being the highest and lowest values of K_n in the system, and similarly $\mu_+$ ($\mu_-$) being the highest (lowest) value of the shear modulus. Milton (1981) presented examples of correlated bounds where the correlations were introduced specifically through spatial correlation functions. But here we introduce correlations instead through the laminated grains. The bounds (4), (5), (8), and (9) are then correlated Voigt and Reuss bounds because of the assumed internal grain-like structure.

We see in Figures 1 and 2 that these bounds (XR and XV) for the polycrystalline case are fairly substantial improvements over the uncorrelated Hashin-Shtrikman bounds (HS$^\pm$), which are themselves substantial improvements over the uncorrelated version of the Voigt and Reuss bounds (the Voigt bound is not shown here, but is just a straight line in each plot between the end points of these curves).

A correlated version of the Hashin-Shtrikman bounds can be computed also, as has been shown by Peselnick and Meister (1965) and Watt and Peselnick (1980) (see Appendix A for the details of these formulas, but not their derivation). We see that these bounds are very tight indeed in comparison to all the others considered here. In particular, note that K_R computed from (4) falls outside the correlated Voigt and Reuss bounds (curves XV and XR) of Figure 1.

For contrast, Figures 1 and 2 also plot another set of bounds derived by Dederichs and Zeller (1973) that is also intended for use in uncorrelated systems (see Appendix B for the formulas and a brief discussion). The DZ bounds behave quite differently from those of the correlated bounds XR, XV, PM$^\pm$.It is easy to see why this is so. In the laminates, as the volume fractions become small for one constituent at one end of the curves and for the other constituent at the other end, the low volume fraction constituent is approaching a flat disc-like geometry. It is well-known (Milton, 1981) that in this circumstance results for disc-like inclusions tend to dominate the behavior and, therefore, tend to hug the upper Hashin-Shtrikman bound in the lower left-hand limit, and then to hug the lower Hashin-Shtrikman bound in the upper right-hand limit of the Figures. We see that this is so for the correlated bounds XR, XV, PM$^\pm$. But the DZ$^\pm$ bounds are uncorrelated and do not show this type of behavior at all.

 

PMW Figure 3 Illustrating the graphical construction leading to the optimum parameters for the comparison material of the lower and upper Peselnick-Meister-Watt bounds: (G-,K-), (G+,K+), shown as red circles. The case shown is for the middle point of the examples shown in Figures 1 and 2 (volume fraction of 0.50). Values of the constants entering the expressions (see Appendix A) are: KV = 30.2162, c44 = 7.2727, c66 = 22.0000, 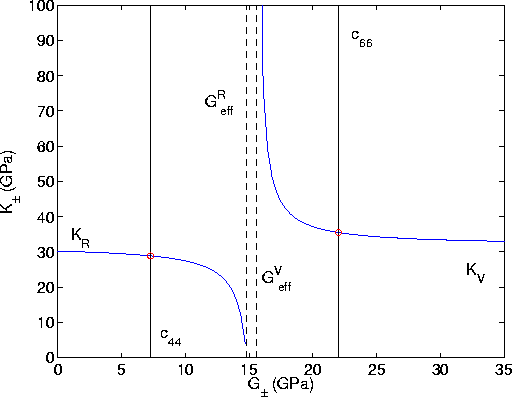$G_{\rm eff}^R = 14.8082$, and $G_{\rm eff}^V = 15.5653$, in units of GPa. The two parts of the blue solid curve are determined by (14) and (16).

The best and also most relevant bounds here are obviously the Peselnick-Meister-Watt bounds (Peselnick and Meister, 1965; Watt and Peselnick, 1980), which are presented and briefly discussed in Appendix A. Figure 3 [following some similar figures in Watt and Peselnick (1980)] shows how the parameter sets for the elastic comparison materials are determined. The allowed regions in Figure 3 are the bounded area in the upper right-hand corner, and the similarly bounded area in the lower left-hand corner. The red circles are therefore the points in the ($G_\pm$,$K_\pm$)-plane that produce the optimum bounds. It is clear that the value of $G_{\rm eff}^V$ plays a very dominant role in the structure of this Figure as the singularity in the blue solid curve occurs exactly at this value.

For the case of constant bulk modulus K_n = K, Figure 3 should be contrasted with Figure 4. Obviously, the structure is much simpler, as the singularities in (22) and (24) have disappeared through direct cancelation with the numerator. It is still the case however that the allowed regions in Figure 4 are the bounded areas in upper right-hand corner, and the lower left-hand corner. Again the red circles are the points in the ($G_\pm$,$K_\pm$)-plane that produce the optimum bounds. However, it is no longer clear from this Figure whether $G_{\rm eff}^V$ is playing any role in the analysis or not.

 

PMWconK Figure 4 As in Figure 3 for the case of constant bulk modulus, in which case KV = KR = K, and 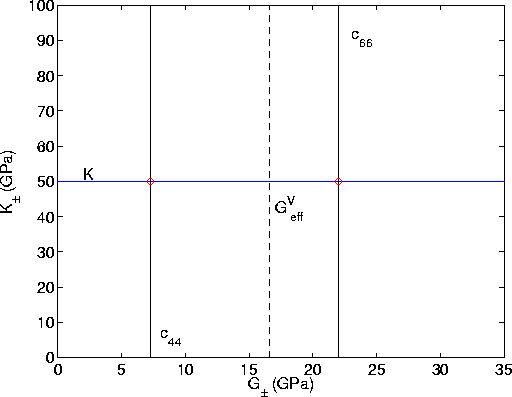$G_{\rm eff}^V = G_{\rm eff}^R$.Values of the constants entering the expressions (see Appendix A) are: K = 50.0000, c44 = 7.2727, c66 = 22.0000, $G_{\rm eff}^V = 16.5546$, in units of GPa.

While attempting to find an answer to this question, the author has spent some effort manipulating the form of the equations for the shear modulus bounds and has found what may be a more enlightening form of these equations. (The derivation will not be given here as it is rather straightforward to find the result again, once the final expression is known.) The resulting simplified formula for the Peselnick-Meister-Watt bounds on overall shear modulus of a polycrystal of laminates when K_n = K is:  

$$\mu_{PM}^\pm = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^V... ...+ \frac{2}{c_{66}+\zeta_\pm}\right)\right]^{-1} - \zeta_\pm,$$ (13)

where  

$$\zeta_\pm = \frac{G_\pm}{6}\left(\frac{9K+8G_\pm}{K+2G_\pm}\... ...uad\hbox{with}\quad G_\pm = c_{44}\quad\hbox{or}\quad c_{66}.$$ (14)

Using standard methods, it is not hard to show that, if instead of optimum values of $\zeta_\pm$, we use $\zeta_\pm = 0$ or $\infty$, then (13) reduces to the formulas (8) and (5) for the correlated Reuss and Voigt bounds on the polycrystal's overall shear modulus.

We see that $G_{\rm eff}^V$ still plays a dominant role here -- in the company of c₄₄ and c₆₆ -- as one of the three values (after multiplication by 2) that are the shear eigenvalues of the elastic system. Furthermore, $G_{\rm eff}^V$ is determined for this case exactly by Eq. (6).