




Next: Relinearization
Up: TOMOGRAPHY
Previous: TOMOGRAPHY
Our velocity model is sampled in  in both depth and x position.
Our total number of model points is approximately seven times
our number of data points. As a result our model is significantly
undeterdetermined. There are several ways to deal with the problem.
One solution would
be to decrease the number of grid points by sampling differently
(coarser regular sampling or some type of irregular sampling).
We can improve the situation by back propagating along fatter rays
or we can add some type of regularization operator.
Potentially the most interesting, and the one chosen for
this paper is to add a regularization operator.
in both depth and x position.
Our total number of model points is approximately seven times
our number of data points. As a result our model is significantly
undeterdetermined. There are several ways to deal with the problem.
One solution would
be to decrease the number of grid points by sampling differently
(coarser regular sampling or some type of irregular sampling).
We can improve the situation by back propagating along fatter rays
or we can add some type of regularization operator.
Potentially the most interesting, and the one chosen for
this paper is to add a regularization operator.
The typical choice for a regularization operator is an isotropic
roughner. This will tend to fill undetermined portions of
the model with isotropic blobs. In many cases this is unrealistic.
Generally velocity follows structure and our structure is laid
down as a series of layers that are later deformed by
tectonic processes. A better choice for our regularization
operator is something that tends to create features that follow structure.
Clapp (2001) showed that this can improve the
velocity estimate for oil exploration targets.
Our regularization operator becomes a steering filter,
a non-stationary filter
which tends to smooth along some predefined dip map. In this
case we used three reflectors to build the dip map from: the surface,
a basement reflector, and the Moho. We measure the dip along
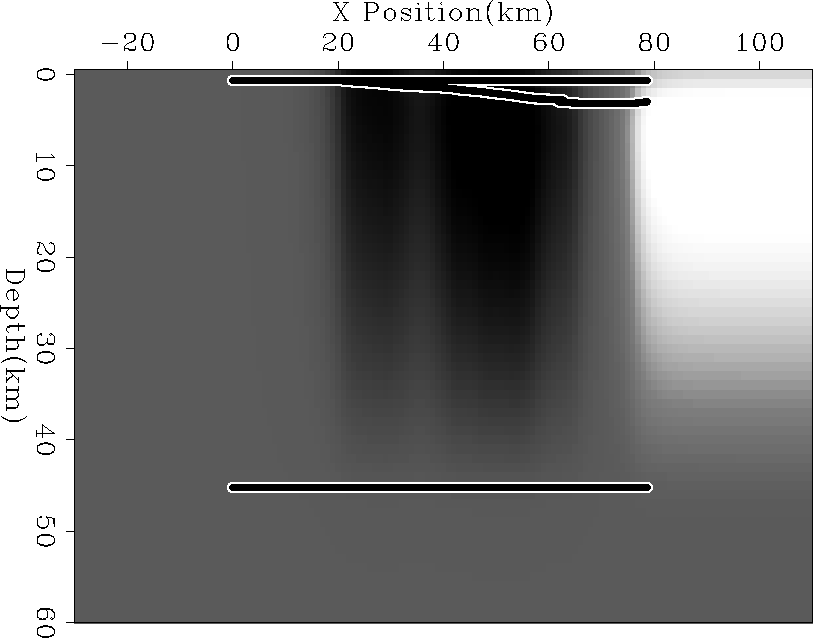
each reflector and then interpolate between them. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the dip field overlain by the reflectors.
shows the dip field overlain by the reflectors.
dips
Figure 4 The dip field and reflectors
used to construct the steering filter operator. The upward dip
on the right edge is due to continuing
the dip present at the edge of the reflectors.
|
|  |





We want to smooth the slowness model,
not the change in slowness that we are inverting
for. As a result our regularization fitting goal becomes
| 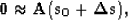 |
(3) |
where 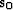 is the initial slowness and
is the initial slowness and 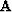 is our steering filter.
This problem converges quite slowly. As a result
we precondition the model using the inverse
of our regularization operator Claerbout (1999).
Our final set of fitting goals become
is our steering filter.
This problem converges quite slowly. As a result
we precondition the model using the inverse
of our regularization operator Claerbout (1999).
Our final set of fitting goals become
| 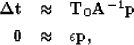 |
(4) |
| |
where 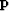 is the preconditioned variable
and
is the preconditioned variable
and  is a twiddle
parameter controlling the amount of smoothing.
Figure
is a twiddle
parameter controlling the amount of smoothing.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the resulting change in velocity and
the updated velocity model. Note how the basin structure
that has now appears in the model.
vel1
shows the resulting change in velocity and
the updated velocity model. Note how the basin structure
that has now appears in the model.
vel1
Figure 5 The left panel shows the
updated velocity model. The right panel is the
change in velocity resulting from 120 iterations
of fitting goals (4).










Next: Relinearization
Up: TOMOGRAPHY
Previous: TOMOGRAPHY
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the dip field overlain by the reflectors.
shows the dip field overlain by the reflectors.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the dip field overlain by the reflectors.
shows the dip field overlain by the reflectors.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the resulting change in velocity and
the updated velocity model. Note how the basin structure
that has now appears in the model.
shows the resulting change in velocity and
the updated velocity model. Note how the basin structure
that has now appears in the model.
