|
rays
Figure 3 The rays forming | 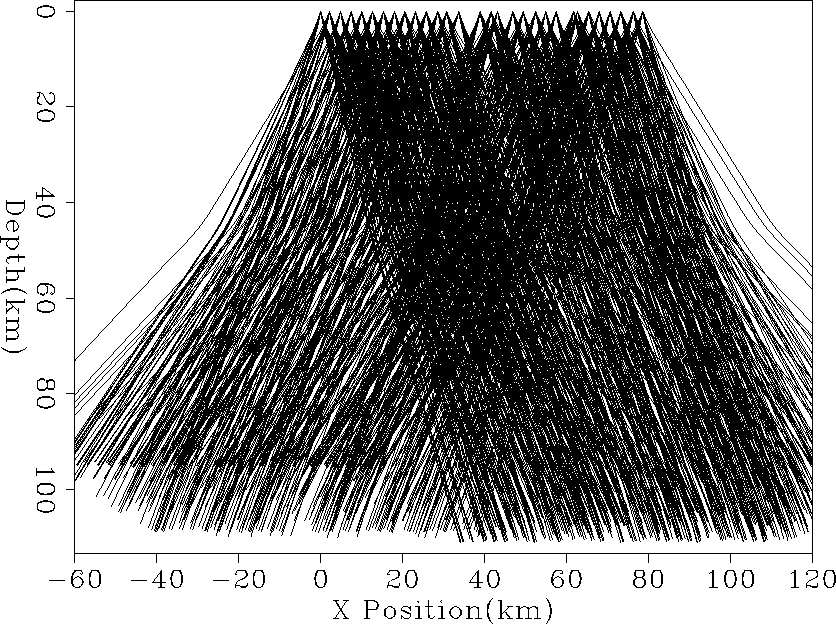 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the rays forming
show the rays forming |
rays
Figure 3 The rays forming |  |
For this experiment we are limiting ourselves
to a 2-D earth model. As shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
our selected set of earthquakes are approximately oriented
along the receiver line. For this experiment we assume
constant velocity out of plane. We do 2-D ray tracing
and then correct all lengths by
,
our selected set of earthquakes are approximately oriented
along the receiver line. For this experiment we assume
constant velocity out of plane. We do 2-D ray tracing
and then correct all lengths by
| (1) |
Each arrival time also has a variance associated
with it. The inverse of these variances form
a noise covariance operator ![]() for the inversion.
We invert for the change in slowness
for the inversion.
We invert for the change in slowness ![]() by
minimizing the fitting goal,
by
minimizing the fitting goal,
| (2) |